Modelování prvku Isokorb

Isokorby jsou speciální prvky používané pro redukci tepelných mostů v betonových konstrukcích. Tento modul se uplatní zejména v případě spojení balkonu s železobetonovou konstrukcí podlaží. Při navrhování takového detailu je třeba uvažovat vhodný numerický model. V tomto článku je popsáno několik metod v programu SCIA Engineer využívajících výpočet pomocí MKP.

Definování modelu

Schöck Isokorb je speciální prvek, který se skládá z ohýbaných vyztužených tyčí přenášejících tah viz detail níže a HTE-kompaktního materiálu přenášejícího tlak. Tepelnou izolaci mezi konstrukcí a balkonem zajišťuje extrudovaný polystyren. Tato součást je schopna přenášet ohybové momenty a posouvající síly v závislosti na zvoleném typu modelu. Torzní momenty však přenášeny být nemohou. Přenos vnitřních sil závisí na stanovené tuhosti prvku.

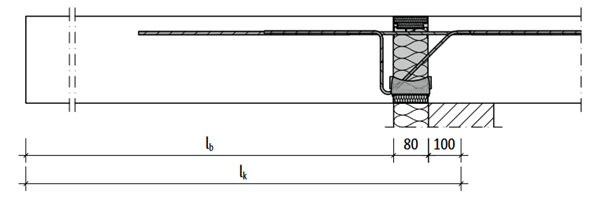
Obecně existují tři možnosti, jak Isokorb ve SCIA Engineer správně modelovat:

• 1) Oddělit balkonovou část od modelu a následně aplikovat výsledné reakce na betonovou konstrukci podlaží
• 2) Použití liniového kloubu s vhodnou tuhostí
• 3) Použití nelineárního kontaktního kloubu

Isokorb - doporučení

Technické informace [1] podle EN1992-1-1 [2] pro Isokorb® obsahují směrnici FEM popisující modelování. Společnost Schöck doporučuje pro návrh Schöck Isokorb® pomocí metody konečných prvků následující přístup:

• Oddělit vnější část od nosné konstrukce budovy.
• Určit vnitřní síly na vnější části podpory s přihlédnutím k tuhosti pružiny na základě doporučených přibližných hodnot pružného uložení pro Schöck Isokorb®:
  • 10 MNm/rad/m pro rotaci
  • 250 MN/m² pro translaci ve vertikálním směru
    
    
  • Zvolte typ Schöck Isokorb® včetně daných návrhových hodnot pro smykovou sílu vEd a moment mEd.
  • Aplikujte vypočtenou smykovou sílu vEd a moment mEd jako vnější liniové zatížení na hranu 2D nosné konstrukce (například stropní desku).
    
    

Případová studie

Modelování a porovnání výsledku je demonstrováno na desce o tloušťce 250 mm o rozměrech 3,0x6,0 m z betonu pevnostní třídy C25/30, na kterou navazuje balkón ze stejného materiálu a tloušťky o rozměrech 2,0x4,0 m. Na celou konstrukci působí rovnoměrné stálé zatížení o velikosti 1,0 kN/m2 a proměnné zatížení 1,5 kN/m2.

Metoda 1 - Oddělení balkónové části od modelu a následné aplikování výsledných reakcí na nosnou betonovou konstrukci
První metoda je založena na oddělení balkonu od zbytku konstrukce a správném definování podpory na jejich vzájemné propojující hraně. Na základě získané reakce je zatížení aplikováno s opačným znaménkem vůči zbytku konstrukce. Tuhosti podpory jsou zřejmé z následujícího obrázku.

Poznámka: Určení reakce z balkónu a předefinování zatížení na hlavní nosnou konstrukci musí být provedeno pro každý zatěžovací stav nezávisle

Reakce z balkónu jsou poté určeny a aplikovány na nosnou konstrukci.

Zatěžovací stav - stálé zatížení

Zatěžovací stav - proměnné zatížení

Jak je vidět, tato metoda je poměrně pracná, protože vyžaduje ruční zadání během zjištění reakcí a jejich předefinování v zatížení na desku. Proto je představena další, efektivnější metoda.

Metoda 2 - Užití liniového kloubu s odpovídající tuhostí
Uživatelsky přívětivější přístup, jak definovat skutečné chování prvku Isokorb, je použití liniového kloubu s příslušnými vlastnostmi v rámci jednoho společného modelu. Liniový kloub je definován na okraji balkónu s následujícími doporučenými vlastnostmi. Používají se pružné tuhosti pro přenos jak smykové síly (uz), tak i ohybového momentu (fix).

Metoda 3 - Použití nelineárního kontaktního kloubu

Předchozí metody jsou založeny na lineární analýze. Třetí metoda využívá tzv. „kontakty“, které jsou ve skutečnosti nelineární funkcí liniového kloubu.

 

 

Na základě předpokladů jsou nelineární funkce pro vertikální posun a rotaci definovány následovně. Jak je znázorněno na obrázku, kloub se chová odlišně v tlaku a tahu. Ve skutečnosti nedochází k přenosu tlakového zatížení a tahové zatížení se chová lineárně. Abyste získali výsledky založené na těchto nelineárních funkcích je pro tuto metodu navíc nutné definovat nelineární kombinaci a spustit nelineární výpočet (vlevo dole: nelineární funkce translace, vpravo dole: nelineární funkce rotace).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Diskuze nad výsledky

Na následujících obrázcích jsou porovnány výsledky všech tří metod. Nejprve zkontrolujme ohybové momenty na konstrukci. Vyhodnocení ohybových momentů je u všech tří metod téměř stejné, jak je v případě lineární analýzy vidět na následujícím obrázku.

 

 

 

 

 

 

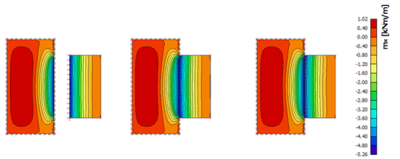
Kromě toho je rozdíl mezi lineární a nelineární metetodou také velmi malý z hlediska ohybových momentů, jak je znázorněno níže (vlevo dole: lineární výsledek, vpravo dole: nelineární výsledek).

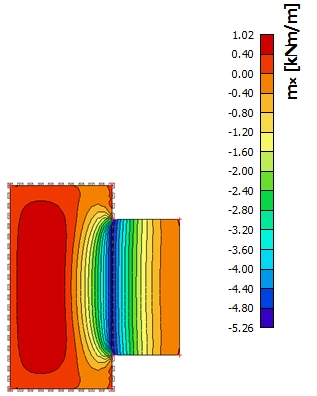
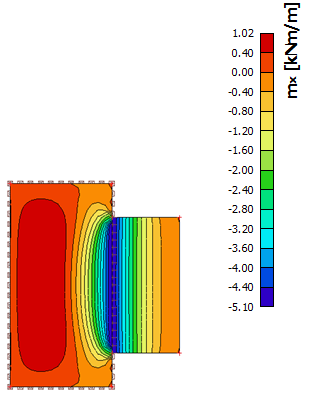
Také v případě deformací existuje dobrá korelace pro lineární výpočet (viz níže).

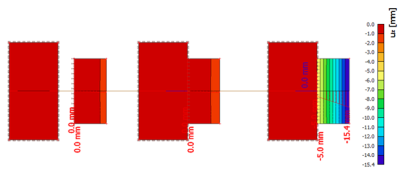
Ale při porovnání výsledků po nelineárním výpočtu lze u třetí metody vidět vysoké průhyby kvůli absenci skutečné výztuže během nelineární analýzy, má v tomto případě významný vliv na průhyb.

Závěr

V tomto článku byly demonstrovány tři možné metody modelování Isokorbu. Jak je patrno, lze použít všechny tři metody, ale s různou měrou úsilí. První metoda vyžadovala ruční předefinování reakcí z volného balkónu na nosnou konstrukci, což může vést k chybám. Třetí nelineární metoda vyžaduje definování skutečné výztuže v konstrukci pro získání správného průhybu balkonu. Druhá metoda je proto dobrým kompromisem při použití liniového kloubu s doporučenými hodnotami tuhosti, který poskytuje dobré výsledky s malým úsilím při modelování.

Reference

[1] Schoeck Isokorb - Technické informace; https://www.schoeck.com/view/2664/Technical_Information_Schoeck_Isokorb_%5B2664%5D.pdf

[2] EN1992-1-1 - Eurokód 2: Navrhování betonových konstrukcí - Část 1-1: Obecná pravidla a pravidla pro pozemní stavby