Udržitelné stavebnictví – experiment s mechanickými spoji pro LLD
Konstrukce těžkého skeletu OC Hustopeče
Analýza rotační tuhosti byla prováděna s dřevěným polotuhým spojením vytvořeným ze systému dvou stojek a příčky z lepeného lamelového dřeva. K tomu byly použity kovové mechanické spojovací prostředky kolíkového typu. Byla zkoušena kombinace svorníků a kolíků spolu s celo-závitovými vruty. Předmětem výzkumu a jeho motivace bylo nahrazení těchto běžně se využívajících spojovacích prostředků za modernější s cílem zlepšení únosnosti takového typu spojení, ale také bylo snahou zkrátit a zjednodušit montážní čas. Každé z těchto dvou typů spojení bylo zatěžováno na úroveň 60, 80 a 100 % hodnoty mezního stavu únosnosti. Následně byla zjišťována rotační tuhost pro každou úroveň zatížení po pěti cyklech zatížení a odtížení. Získané výsledky experimentálního testování byly porovnávány s analytickým předpokladem podle aktuálně platné normy a aplikovány na spoje a detaily u těžkého jednopatrového skeletu v Hustopečích. Jde o obchodní dům, kde střešní konstrukce byla projektována na vysoké zatížení a možné dynamické účinky od provozu hřiště.
1. EXPERIMENTÁLNÍ FYZIKÁLNÍ ANALÝZA PRO OVĚŘENÍ CHOVÁNÍ SPOJŮ A DETAILŮ NOSNÝCH ČÁSTÍ KONSTRUKCE
POPIS KONSTRUKCE A GEOMETRIE
Konstrukční systém experimentu byl vytvořen z polotuhého spojení dvou stojek a příčky. Spojení bylo vytvořeno z kovových mechanických spojovacích prostředků kolíkového typu. Celkově byly vytvořeny dva totožné konstrukční systémy, jejichž rozdíl byl pouze v použitém spojovacím prostředku. Experiment A obsahoval jako spojovací prostředky kombinaci svorníků a kolíků a druhý, experiment B, byl vytvořen z celozávitových vrutů. Pro vytvoření konstrukce bylo použito lepené lamelové dřevo deklarované třídy GL24h. Pro ověření vlastností dřeva byly vytvořeny dílčí testy, které byly zveřejněny v již publikovaném článku Johanides 2022 [1]. Segment stojky měl průřez 100/300 mm a segment příčky měl průřez 100/300 mm. Materiál spojovacích prostředků byl také experimentálně ověřen pevností v tahu ve výše uvedeném článku. Experiment A byl zhotoven z kombinace svorníků a kolíků, ocel třídy 10.9. Vnější průměr závitové tyče byl 8 mm, vnitřní průměr 7,25 mm. Délka svorníku byla 360 mm a délka kolíku 300 mm.
V tomto experimentu byly spojovací prostředky předvrtány vrtákem o průměru 8 mm, ideou bylo vytvoření spojení bez počátečního prokluzu. Materiál spojovacích prostředků v experimentu B, celozávitové vruty, byla ocel třídy 10.9. Vnější průměr vrutu byl 8 mm, vnitřní průměr vrutu byl 5 mm a délka 300 mm. Tento spojovací prostředek byl předvrtán vrtákem o průměru 5 mm, také z důvodu minimalizování počátečního prokluzu spojení.
Rozmístění spojovacích prostředků v obou experimentech bylo totožné. Nacházely se na jedné symetrické kružnici o poloměru r = 90 mm s počtem 10 ks. Rozmístění bylo určeno podle Koželouh 1998 [2], viz obrázek 1.
Pro testování experimentálních testů byla zhotovena externí ocelová konstrukce, která zajišťovala okrajové podmínky. Schéma samotného experimentálního testu je uvedeno na obrázku 2.
POPIS PRŮBĚHU ZATĚŽOVÁNÍ A UMÍSTĚNÍ SNÍMAČŮ DRÁHY
Cílem statických cyklických testů bylo zkoumání chování rámového spojení při různých úrovních zatížení a na základě získaných dat možné stanovení hodnot rotační tuhosti pro jednotlivé úrovně zatížení.
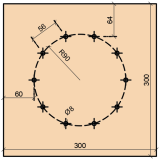
Obr. 1 – Rozmístění spojovacích prostředků
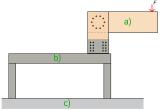
Obr. 2 – Schematické znázornění experimentu: (a) zkoumané rámové spojení, (b) ocelová konstrukce, (c) železobetonová podlaha
Myšlenka takového testování je postavena na praktickém požadavku. To znamená, že v praxi se stavební konstrukce navrhují na mezní stavy. V reálně zabudované konstrukci nesmí být hodnota mezního stavu únosnosti překročena, protože hrozí trvalé poškození nosné konstrukce, případně její kolaps. Z tohoto důvodu nebyl určen význam zkoumání rotační tuhosti spojení za hranicí mezního stavu únosnosti. Pro experimentální testování byly zvoleny tři úrovně zatížení – 60, 80 a 100 % hodnoty mezního stavu únosnosti.
Hodnoty rotační tuhosti polotuhého spojení byly získány odseparováním jednotlivých vnějších vlivů. První vnější činitel ovlivňující rotační tuhost spoje bylo spojení dolní části stojin s ocelovou konstrukcí. Pro získání náklonu stojiny od ocelové konstrukce byl umístěn horizontální snímač S2, obrázek 3.
Druhou složkou byly jednotlivé deformace segmentů konstrukce. Jejich deformaci bylo možno spočítat silovou metodou. Odečtením jednotlivých složek deformace od celkové deformace z vertikálně umístěného snímače S1, obrázek 3, dostaneme skutečnou hodnotu deformace způsobenou rotační tuhostí polotuhého spojení.
EXPERIMENTÁLNÍ TESTOVÁNÍ
Jednotlivé experimenty byly testovány v experimentálním stavebním a diagnostickém centru VŠB – Technická univerzita Ostrava. Na obrázku 4 nahoře je zobrazen experiment A (a), kombinace svorníků a kolíků, dole pak experiment B (b), celozávitové vruty před statickým cyklickým zatěžováním. Zatížení bylo do spojení aplikováno pomocí ocelového válce o průměru 50 mm. Pod tento válec byla vložena gumová podložka o tloušťce 10 mm, aby se zamezilo lokálnímu poškození dřeva při zatěžování.
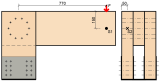
Obr. 3 – Zobrazení umístění snímačů deformace, vlevo čelní pohled, vpravo pohled z boku.


Obr. 4 – Experimentální vzorky: (a) experiment A, kombinace svorníků a kolíků, (b) experiment B, celozávitové vruty (b).
Tabulka 1 – Výsledky hodnot rotační tuhosti.
|
Metoda |
Druh spojovacího prostředku |
|
Hodnota [MNm/rad] |
Porovnání [%] |
|
ČSN EN 1995-1-1 [3] |
Svorníky a kolíky |
kr,u,EC5 |
0.323 |
- |
|
kr,u,EC5,1 |
0.299 |
-8 |
||
|
kr,u,EC5,2 |
0.293 |
-10 |
||
|
kr,test,60 |
2.198 |
+85 |
||
|
kr,test,80 |
1.055 |
+31 |
||
|
kr,test,100 |
0.404 |
+20 |
||
|
ČSN EN 1995-1-1 [3] |
Celozávitové vruty |
kr,u,EC5 |
0.323 |
- |
|
kr,u,EC5,1 |
0.206 |
-57 |
||
|
kr,u,EC5,2 |
0.202 |
-60 |
||
|
kr,test,60 |
0.386 |
+16 |
||
|
kr,test,80 |
0.313 |
-3 |
||
|
kr,test,100 |
0.896 |
+64 |
VÝSLEDKY EXPERIMENTÁLNÍHO VÝZKUMU
V tabulce 1 se nacházejí získané hodnoty z experimentálního měření, které jsou porovnávány s návrhovými hodnotami získanými pomocí normy ČSN EN
1995-1-1 [3]. Každá hodnota, pro jednotlivé úrovně zatěžování, byla získána průměrem hodnot z pěti provedených cyklů zatěžování. V tomto srovnání je vzata jako referenční hodnota hodnota kr,u,EC5 0,323 MNm/rad, která byla získá- na dosazením normových materiálových vlastností do vztahu výpočtu modulu prokluzu podle výše uvedené normy. Jako další hodnota figuruje v tabulce kr,u,EC5,1. Tato hodnota byla získána použitím skutečného naměřeného průměru jádra spojovacího prostředku a skutečně naměřené hustoty dřeva. Poslední hodnotou kr,u,EC5,2 je hodnota získaná použitím skutečného průměru jádra spojovacího prostředku a normové hodnoty hustoty dřeva podle jeho pevnostní třídy.
Na obrázku 5 a 6 jsou v závislosti na zatížení zobrazeny průběhy rotační tuhosti jednotlivých spojení. V tomto obrázku jsou také naznačeny hodnoty rotační tuhosti vypočtené pro mezní stav únosnosti (MSÚ) a mezní stav únosnosti bez použitých parciálních součinitelů spolehlivosti (MSÚ 1).
Na obrázku 7 jsou zobrazeny křivky vyjadřující průběh závislosti rotační tuhosti na zatížení pro jednotlivé spojovací prostředky. Z obrázku je zřejmé, že se zvyšujícím zatížením rotační tuhost spojení vytvořeného vruty mírně narůstá, zatímco při kombinaci svorníků a kolíků klesá.
Na obrázku 8 je k nahlédnutí numerický model testovaného rámového rohu. Jedná se o součást pro rámový těžký skelet. Cílem těchto testů (byly použity různé typy spojovacích prostředků jak v samotném rohu, tak i v externích přípojích k ocelovým prvkům) bylo stanovení rotačních tuhostí a celková analýza chování tohoto typu spoje.
Na obrázku 9 jsou fotografie z laboratoří Fakulty stavební VŠB TU Ostrava.
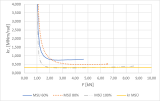
Obr. 5 – Průběh rotační tuhosti v závislosti na vnášené síle, kombinace svorníků a kolíků.

Obr. 6 – Průběh rotační tuhosti v závislosti na vnášené síle, celozávitové vruty.
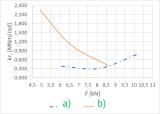
Obr. 7 – Porovnání průběhu rotační tuhosti jednotlivých spojovacích prostředků: (a) šroub, (b) svorník

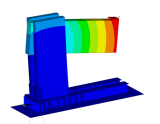
Obr. 8 – Geometrie a sítě konečných prvků rámového rohu (a), celkové deformace řešené konstrukce (b).


Obr. 9 – Příprava testu rámového rohu (a), ukázka deformace rámového rohu po zatížení (b).
ZÁVĚRY
Experimentálním testováním spoje vytvořeného ze standardně využívané kombinace svorníků a kolíků, experiment A, byla prokázána bezpečnost a spolehlivost spoje při zatěžování na mezní stav únosnosti. Z pohledu rotační tuhosti dosahuje tento spoj po celou dobu zatěžování hodnot vyšších, než je předpoklad normy pro mezní stav únosnosti.
Experimentálním testováním spoje vytvořeného z celozávitových vrutů, experiment B, byla prokázána také bezpečnost a spolehlivost spoje při zatěžování na mezní stav únosnosti. Z pohledu rotační tuhosti nedosahuje tento spoj hodnot vyšších, než je předpoklad normy pro mezní stav únosnosti pro úroveň zatížení 80 % MSÚ. Testování tohoto experimentu naznačuje, že pro dosažení přesnějšího výsledku rotační tuhosti podle Eurokódu 5 [3] je nutné použít pro výpočet modulu prokluzu průměr dříku spojovacího prostředku. Případně lze použít průměr dříku spojovacího prostředku a skutečnou naměřenou hustotu dřeva. Vzhledem k tomu, že z praktického hlediska je obtížné získávat skutečnou naměřenou hustotu dřeva, je podle dat získaných v tomto příspěvku dostatečně přesné použití průměru dříku spojovacího prostředku a normové hodnoty hustoty dřeva.
Problematika určování únosnosti spojů dřevěných konstrukcí podle evropských norem pro navrhování dřevěných konstrukcí Eurokód 5 [3] je neustále ve vývoji. K tomuto trendu by mohly přispět i navrhované experimenty, které byly zaměřeny na stanovení rotační tuhosti polotuhého spojení dřevěné příčky a stojky vytvořeného pomocí mechanických spojovacích prostředků kolíkového typu.
Údaje z experimentů lze využít pro praktické navrhování takového typu polotuhého spojení z hlediska rotační tuhosti. Autor, Marek Johanides, věnoval samostatné články problematice únosnosti [4], duktility [1] a rotační tuhosti [5] tohoto typu spojení.
Předností dřeva je jeho obnovitelnost a charakter, který lidé znají a vyhledávají po tisíciletí své existence.
Dřevní hmota má vzhledem ke své objemové hmotnosti velmi dobré pevnostní vlastnosti podélně s vlákny. Pokud je stavební prvek mohutného charakteru, je i požární odolnost vysoká, a pokud je doplněna pasivními a aktivními protipožárními prvky, je možné realizovat vícepatrové domy na bázi dřeva, jmenovitě Brumunddal Norsko.
Dřevo jakožto přírodní rostlý materiál je náchylný na biologický rozpad a napadení (dřevokazné houby a hmyz). V případě, že se dřevo a detaily jeho spojů dostatečně chrání, mají tyto stavby potenciál životnosti stovek let (most Kapellbrücke CH).
2. VYUŽITÍ MOŽNOSTÍ NUMERICKÝCH MODELŮ NA REALIZOVANÉ STAVBĚ OBCHODNÍHO DOMU COOP HUSTOPEČE
TEŽKÉ SKELETY V UDRŽITELNÉM STAVEBNICTVÍ
Těžké skelety na bázi dřeva jsou v dnešní době pro vícepatrovou nebo těžkou zástavbu vyhledávané. Je to především dáno tendencí mít průmysl, jehož je stavebnictví součástí, co nejvíce udržitelný, a to především vzhledem ke zdrojům a energiím se zahrnutím šetrnosti k přírodě a obnovitelnosti zdrojů. Dřevo je přírodní materiál a jako takový má své přednosti a také vlastnosti, které je nutné vylepšit pro dosažení potřebných parametrů daných typem a užitím stavby.
S vývojem moderního zpracování dřeva (GLT, CLT atd.) doplněného o vývoj detailů vysoko únosných spojů (ocel, epoxidové pryskyřice, skelná vlákna a kombinace těchto materiálů) spolu s výkonnými numerickými simulacemi doplněnými o normativní zkušenosti a fyzikální testy je možné navrhovat a optimalizovat stavbu jako celek a tím docílit a umožnit stavbám na bázi dřeva dosáhnout nových objemů, tvarů a forem. Na obrázku 10 je vizualizace možného využití střechy řešeného skeletu.
V tomto článku je cílem představit možnosti těžkých skeletů. Obecně se dají nosné konstrukce dle statického systému rozdělit na rámový, stěnový a příhradový systém. Rámový systém je ze své podstaty nejméně tuhý a pro spoje u dřevěných konstrukcí to platí násobně. Stěnový systém je velmi tuhý a lze o něm uvažovat pro výškové stavby (železobetonová nosná jádra mrakodrapů). Příhradový systém je poměrně lehký, má dobrou tuhost a také u něho je dominantním místem spoj (kumulují se zde vysoké uzlové síly) mezi jednotlivými prvky jako u rámových systémů. Stěnový systém při vhodné geometrii nemá tak vysoké uzlové síly na spoje a tím také vysoké lokální namáhání detailů spojů. Na obrázku 11 je schéma konstrukce haly o rozměrech zhruba 30,6 × 46,3 × 6 m, půdorys je dominantně obdélníkový s bočními schodišti. Stavba je navázána na boční servisní konstrukci zázemí haly.

Obr. 10 – Vybraná nerealizovaná vizualizace obchodního domu COOP Hustopeče.
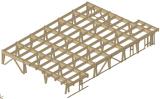

Obr. 11 – Kombinovaný systém, schéma těžkého skeletu – rámy a příhrady COOP Hustopeče.

Obr. 12 – Externí pohled na vstup do obchodního domu.

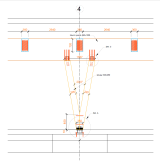
Obr. 13 – Interiér obchodního domu v provozním stavu (vlevo), detail kotvení „V“ sloupu (vpravo).


Obr. 14 – Hrubá stavba a pohled na prvky skeletu (vlevo), vrut do dřeva a oceli (vpravo).

Obr. 15 – Vnitřní síly na vybraný systém nosných prvků skeletu.

Obr. 16 – Smontovaná hlavní nosná konstrukce haly obchodního domu.
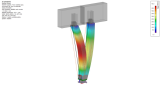

Obr. 17 – Numerický model nosných prvků skeletu.


Obr. 18 – Vnitřní síly na vybraný systém nosných prvků skeletu.
COOP VE HUSTOPEČÍCH
Jedná se o jednopodlažní stavbu nákupního centra s těžkou střechou uvažovanou jako skatepark. Hlavní nosný systém je založen na sloupech a střešní tuhé desce s trámy a průvlaky. Vybrané dřevěné prvky jsou blokově lepené a dosahují šířky 480 mm. Statické schéma stavby a její prostorovou tuhost zajišťují „A“ a „V“ sloupy, které jsou sestaveny v pravoúhlých rastrech s tuhou střešní rovinou. Sloupy jsou dominantně zatíženy tlakem a tahem. Rámový roh je tvořen uzavřeným trojúhelníkem vzhledem k průvlaku a k zemi. Obrázek 12 je náhledem na opláštěnou konstrukci haly obchodního domu.
Obrázek 13 – levá část je náhledem na vybavený interiér obchodního domu a je zde možné porovnat začlenění nosné konstrukce do schématu potřebného pro provoz obchodu. Konstrukce i přes svou mohutnost působí v rámci prostoru přirozeným dojmem s akcentem na přírodní charakter hlavních prvků konstrukce haly. Vzhledem k rozměrům prvků a skrytým spojům bude konstrukce vykazovat reálně vysokou odolnost na účinky požáru. Na pravém obrázku 13 je grafická CAD podoba sloupu a jeho kotvení s návazností na další prvky konstrukce haly.
Obrázek 14 – v levé části fotografie můžeme vidět jeden z hlavních prvků dřevěného skeletu „V“, rámový systém napojený na průvlak. Průvlak je rozměru 480 × 1 200 mm, jedná se o blokově lepený prvek z lepeného lamelového dřeva třídy GL28h. Na průvlak jsou napojeny trámy také blokově lepené o rozměru průřezu 360 × 720 mm GL28h. Trám je k průvlaku kotven pomocí vrutů s celým závitem SFS průměru 13 × 500 mm, kde na jeden spoj připadá 10 kusů těchto vrutů. Spoj je navržen na přibližně 211 kN smykové síly od zatížení střechou se zahrnutím klimatických a užitných zatížení.
Na pravém obrázku je k nahlédnutí mechanický spojovací prostředek do dřeva a oceli. Tímto samovrtným kolíkem je možno bez předvrtání spojovat dřevěné prvky s ocelovými pláty. Spoj vykazuje vysokou únosnost a tuhost. Tyto spoje byly použity v hlavách a patách sloupů.
Obrázek 16 zachycuje hlavní rastr nosného systému dřevěného jednopodlažního skeletu před opláštěním. Spodní obrázek 17 dává náhled na vybrané numerické modely hlavních nosných prvků. Levý obrázek vykresluje vybraný vlastní tvar stability pro zadané zatížení. Tento vlastní tvar je dán lokálním vybočením sloupu. Prostřední obrázek ukazuje použitý spojovací prostředek vrutu s celým závitem, který byl použit pro zvýšení únosnosti dřeva v otlačení kolmo na vlákna a také pro přenos smykových sil, viz obrázek 15, a sepnutí dřevní masy v tahu kolmo na vlákna. Pravý obrázek znázorňuje nosný rám typu „A“ s příhradovým působením.
Toto průhledové zobrazení ukazuje způsob numerického modelování daného systému dřevěných a ocelových prvků. Numerický model byl sestaven ze skořepinových a prutových prvků [7], tento model zohledňuje kontaktní podloží, fyzikální a geometrickou nelinearitu. Dále je zde uvažováno s prokluzy spojů a konstrukční nelinearitou spolu s imperfekcemi. Takto uvažovaný model může být řešen samostatně nebo jako součást globálního modelu. V případě zakomponování samostatného modelu do globálního numerického modelu se zvyšuje náročnost řešení. Ale vzájemná interakce je reálnější, protože okrajové podmínky jsou dány „reálným“ vymodelováním napojení jednotlivých prvků spoje.
Obrázek 18 je součástí levé konstrukce z obrázku 17, konkrétně jeho patního spoje, kde levý obrázek znázorňuje kontaktní napětí v oblasti napojení ocelového třmenu na železobetonový podklad. Kontaktní napětí zde dosahuje hodnoty cca 10,20 MPa pro tlakovou sílu cca 1 144 kN. Na pravém obrázku je vlastní tvar stability pro vybrané zatížení, které by mělo vyvozovat maximální tlak. Je zde patrné lokální vyboulení delší stěny uzavřeného boxu ocelového prvku. Vlastní tvary zde uvedené se pohybují okolo hodnoty 2,7násobku vstupního zatížení. Výhodou komplexních numerických modelů je výpočet nelineárních tvarů stability se zohledněním globální tuhosti.
Obrázek 19 znázorňuje vybranou část nosného systému dřevěného skeletu z celého numerického prutového modelu. Tento numerický model je sestaven z objemových a prutových konečných prvků. Jedná se o kontaktní úlohu se zohledněním ortotropie dřeva s bilineárními pracovními materiály dřeva a oceli.
Obrázek 20 – levá část zobrazuje konečně prvkovou síť průvlaku a trámů spolu s ocelovými vruty. Napojení se realizuje přes kontakty s třením a zvoleným prokluzem. Zobrazený numerický model je součástí globálního modelu, viz obrázek 19. Místo pro zasíťování řešeného detailu napojení ve smyku bylo vybráno tak, aby do spoje byla vnášena maximální síla podle prutového modelu cca 211 kN. Pravý obrázek je detail pohledu na vruty, které jsou instalovány do průvlaku a trámu a tvoří smykový spoj.
Zde je zobrazeno napětí, které dosahuje cca 1 019 MPa v oblasti přechodu mezi trámem a průvlakem. Toto místo spoje se chová jako příhrada dle předpokladů, podle kterých tento spoj byl vyvinut, a je používán ve stavební praxi již desítky let.
Obrázek 21 – levá část zobrazuje napětí ve smyku pro prvek průvlaku 480 × 1 200 mm. Napětí ve smyku dosahuje v místě přechodu trámu a průvlaku hodnoty cca 2 MPa. Napětí pro rostlé dřevo pro tento způsob a směr namáhání je podle normy 2,7 MPa v charakteristické hodnotě. Fyzikální hodnota pevnosti ve smyku pro zmíněné namáhání se pohybuje od 3 MPa až 6 MPa. Pravý obrázek v napětí na trámu 360 × 720 mm se chová obdobně jako levý obrázek průvlaku. Při analýze byly zohledněny také možné nepřesnosti v kontaktním napojení mezi průvlakem a trámem. V rámci variant numerických modelů bylo uvažováno s okamžitým kontaktem mezi průvlakem a trámem a také s mezerou, která nebude ani po zatížení v kontaktu mezi prvky trámu a průvlaku.
Na analyzovaných modelech bylo zjištěno, že vliv kontaktu mezi čelem trámu a plochou průvlaku nemá významný vliv pro napětí na vrutech přibližně do 7 % z napětí Von Mises. Při plném kontaktu trámu a průvlaku je znatelné zvýšení kontaktního napětí kolmo na vlákna, může dosahovat lokálně 5,0 MPa.
Obrázek 22 a jeho řez vykresluje rozdělení napětí kolmo na vlákna. Pro zatížení na konci trámu 211 kN je napětí v tahu kolmo na vlákna v lokálním maximu 2,70 MPa a v tlaku kolmo na vlákna v lokálním minimu 5 MPa. Jde o hodnoty na hranici fyzikální pevnosti dřeva. Vzhledem k jejich povaze se jedná částečně o numerický extrém způsobený zjednodušením v modelování a volbou materiálového modelu, který nemůže zcela popsat chování (anisotropii) dřeva. V zásadě ale tyto extrémy vzniknou a kumulují se v oblasti křížení vrutů a jejich přechodu z trámu do průvlaku. Spodní tlak kolmo na vlákna pro průvlak je dán numerickým modelem, který uvažuje okamžitý kontakt trám-průvlak a je způsoben natočením trámu a jeho páčením kolem jeho spodní hrany do průvlaku. Zde se vlivem tření mírně mění i zatížení vrutů, protože je jim nucen bod otáčení. Na pravém obrázku 22 je znázorněna deformace trámů a průvlaku. Minimum je přibližně 9 mm a maximum 12 mm. Vzájemný prokluz mezi čelem trámu a průmětem čela trámu na průvlak je přibližně 0,977 mm od smykové maximální síly 211 kN na spoj.
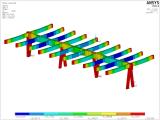
Obr. 19 – Deformace vybraného průvlaku se zahrnutím detailu spoje na smyk, model v prostředí ANSYS [6].

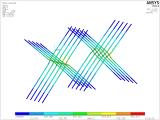
Obr. 20 – Detail numerického modelu konečné prvkové sítě a vrutů.
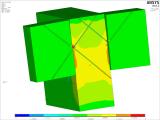
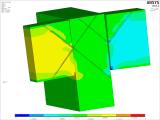
Obr. 21 – Smykové napětí na průvlaku a trámu vybraného detailu spoje.
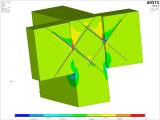
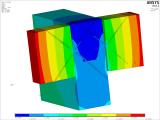
Obr. 22 – Detail numerického modelu napětí v tahu kolmo na vlákna a deformace spoje.
POUŽITÍ NUMERICKÝCH METOD V PRAXI
Shrnutím k výpočtu těžkých skeletů a jejich detailů by bylo, že použití numerických metod je výhodné pro detaily a konstrukce, které jsou ve své povaze nové nebo jsou vysoce zatíženy a jejich geometrie a způsob kotvení jsou méně známy. Numerické metody musí být doplněny o normový způsob řešení, odbornou literaturu a v nutném případě také o fyzikální měření. Nezbytnou součástí je také konzultace se staršími odborníky v dané oblasti.
V případě, že je k dispozici tato škála přístupů k řešení nových typů spojů a konstrukcí, je možné sestavovat náročné objekty a optimalizovat jejich systém a detaily tak, aby jejich pevnost a tuhost byla doprovázena vhodnou odezvou duktility.
V současné době, kdy je vhodné a nutné brát ohled na stav planety a její zdroje, bez nichž civilizace není schopna ve své nynější podobě setrvat, může vývoj v oblasti staveb na bázi dřeva přinést ekologické a odbouratelné materiály, které jsou nejen krásné, ale také plně funkční a schopné snést vysoké zatížení. Tím zahrnout do realizace širokou oblast stavebnictví od rodinné výstavby přes komplexy budov až po vícepatrové výškové budovy (příkladem může být Skandinávie, Rakousko a Anglie).
LITERATURA
[1] Johanides, M.; Lokaj, A.; Mikolasek, D.; Mynarcik, P.; Dobes, P.; Sucharda, O. Timber Semirigid Frame Connection with Improved Defor- mation Capacity and Ductility. Buildings 2022, 12, 583. https://doi. org/10.3390/buildings12050583.
[2] Timber Structures According To Eurocode 5; STEP 1: Design and construction materials; Translated by Bohumil Kozelouh; KODR: Zlin, Czech Republic, 1998; ISBN 80-238-2620-4 (In Czech).
[3] ČSN EN 1995-1-1. Eurocode 5: Design of Timber Structures – Part 1-1: General – Common Rules and Rules for Buildings; Czech Standards Institute: Praha, Czech Republic, 2006.
[4] Johanides, M.; Lokaj, A.; Dobes, P.; Mikolasek, D. Numerical and Experimental Analysis of the Load-Carrying Capacity of a Timber Semi-Rigid Dowel-Type Connection. Materials 2022, 15, 7222. https://doi.org/10.3390/ma15207222.
[5] Johanides, M.; Lokaj, A.; Dobes, P.; Mikolasek, D. Numerical and Experimental Analysis of the Rotational Stiffness of a Timber Semi-Rigid Dowel-Type Connection. Materials 2022, 15, 5622. https://doi.org/10.3390/ma15165622.
[6] AnsysTM, dostupné na www.ansys.com.
[7] Scia Engineer, dostupné na www.scia.net.
Autoři:
Ing. Marek Johanides, Ph.D., specializuje se na dřevěné a ocelové konstrukce s ohledem na numerické modelování doplněné fyzikálním měřením. Je členem Experimentálního a diagnostického stavebního centra Fakulty stavební, VŠB – Technická univerzita Ostrava.
Prof. Ing. Antonín Lokaj, Ph.D., specializuje se na dřevěné a ocelové konstrukce s ohledem na aplikovaný výzkum a vývoj detailů spojů kombinovaných konstrukcí. Působí jako vedoucí katedry konstrukcí a proděkan pro rozvoj na Fakultě stavební, VŠB – Technická univerzita Ostrava.
Ing. David Mikolášek, Ph.D., specializuje se na dřevěné, ocelové a kompozitní konstrukce s ohledem na numerické modelování validované fyzikálním měřením. Je členem katedry konstrukcí Fakulty stavební, VŠB – Technická univerzita Ostrava.
Ing. Pavel Dobeš, Ph.D., specializuje se na stavební konstrukce, detaily s ohledem na jejich diagnostiku, měření a výpočet. Je členem Experimentálního a diagnostického stavebního centra Fakulty stavební, VŠB – Technická univerzita Ostrava.
Ing. Pavel Vlček, Ph.D., specializuje se na oblast občanské výstavby se zahrnutím nových poznatků konstrukčních systémů do stavební praxe. Je členem katedry pozemního stavitelství Fakulty stavební, VŠB – Technická univerzita Ostrava.
Ing. Robert Martinek je specialistou v oboru dřevěných konstrukcí se zaměřením na návrh, optimalizaci a výrobu dřevěných detailů a konstrukcí. Působí jako jednatel ve společnosti EXTEN CZ.
Časopis byl otištěn v časopise KONSTRUKCE 4/2023 (https://konstrukce.cz).