CONSTRUCTION DURABLE – UNE EXPÉRIENCE AVEC DES JOINTS MÉCANIQUES POUR LE BOIS LAMELLÉ-COLLÉ
L’ossature lourde d’un centre commercial dans la ville de Hustopeče
Cet article traite de l’analyse de la rigidité en rotation d’un assemblage semi-rigide en bois formé par un système de deux étais en lamellé-collé et d’une barre transversale. Pour ce faire, des fixations mécaniques métalliques à goupilles ont été utilisées. Une combinaison de boulons et de goupilles a été testée, ainsi que des vis entièrement filetées. Le sujet de la recherche et sa raison d’être étaient le remplacement de ces attaches couramment utilisées par des attaches plus modernes afin d’améliorer la capacité de charge de ce type d’assemblage, ainsi que pour raccourcir et simplifier le temps de montage. Chacun de ces deux types d’assemblage a été soumis à des charges allant jusqu’à 60, 80 et 100 % de l’état limite ultime. Ensuite, la rigidité en rotation pour chaque niveau de charge a été déterminée après cinq cycles de charge et de décharge. Les résultats obtenus lors des essais expérimentaux ont été comparés à l’hypothèse analytique selon la norme actuellement en vigueur et ont été appliqués aux assemblages et aux détails d’une ossature lourde d’un étage d’un grand magasin dans la ville de Hustopeče. La structure du toit du grand magasin a été conçue pour supporter des charges élevées et d’éventuels effets dynamiques liés au fonctionnement d’une aire de jeux.
1. ANALYSE PHYSIQUE EXPÉRIMENTALE POUR VÉRIFIER LE COMPORTEMENT DES JOINTS ET DES DÉTAILS DES PARTIES PORTEUSES DE LA STRUCTURE
DESCRIPTION DE LA STRUCTURE ET SA GÉOMÉTRIE
Le système structurel de l’expérience consistait en un assemblage semi-rigide de deux poteaux et d’une barre transversale. L’assemblage a été réalisé au moyen d’attaches mécaniques métalliques de type goupille. Dans l’ensemble, deux systèmes structurels identiques ont été créés, la seule différence résidant dans les fixations utilisées. L’expérience A comportait une combinaison de boulons et de goupilles, tandis que l’autre, l’expérience B, utilisait des vis entièrement filetées. Du bois lamellé-collé de la classe déclarée GL24h a été utilisé pour la structure. Pour vérifier les propriétés du bois, des tests partiels ont été créés, qui ont déjà été publiés dans l’article Johanides 2022 [1]. Le segment de poteau avait une section droite de 100 x 300 mm et le segment de barre transversale avait une section droite de 100 x 300 mm. La résistance à la traction du matériau des attaches a également été vérifiée expérimentalement dans l’article susmentionné. Dans l’expérience A, une combinaison de boulons et de goupilles, de l’acier de qualité 10.9, a été utilisé. Le diamètre extérieur de la barre filetée était de 8 mm, le diamètre intérieur de 7,25 mm. Le boulon mesurait 360 mm de long et la longueur de la goupille était de 300 mm.
Dans cette expérience, les fixations ont été pré-percées avec un foret de 8 mm. L’idée était de créer un assemblage sans qu’il y ait de glissement initial. Le matériau des fixations de l’expérience B, les vis entièrement filetées, était composé d’acier de qualité 10.9. Le diamètre extérieur de la vis était de 8 mm, le diamètre intérieur de 5 mm et la longueur de 300 mm. Cette fixation a été pré-percée avec un foret de 5 mm de diamètre, également pour minimiser le glissement initial dans l’assemblage.
Les positions des fixations étaient identiques dans les deux expériences. Dix fixations ont été disposées sur un cercle symétrique d’un rayon de r = 90 mm. Les positions ont été déterminées selon Koželouh 1998 [2], voir Figure 1.
Une structure externe en acier a été construite pour fournir des conditions limites pour les tests expérimentaux. La figure 2 présente un schéma de l’essai expérimental proprement dit.
DESCRIPTION DU PROCESSUS DE CHARGE ET EMPLACEMENT DES CAPTEURS DE DÉPLACEMENT
L’objectif des essais statiques cycliques était d’étudier le comportement de l’assemblage à différents niveaux de charge et, sur la base des données obtenues, de déterminer les valeurs de rigidité en rotation pour les différents niveaux de charge.
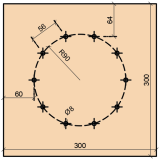
Fig. 1 - Disposition des fixations
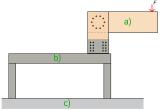
Fig. 2 - Représentation schématique de l’expérience: (a) assemblage étudié, (b) structure acier, (c) sol en béton armé
L’idée de ces tests repose sur une exigence pratique. Cela signifie que, dans la pratique, les structures de génie civil sont conçues pour les états limites. Dans une véritable structure intégrée, la valeur d’état limite ultime ne doit pas être dépassée, car il y aurait un risque de dégâts permanents à la structure porteuse ou d’effondrement. Par conséquent, la rigidité en rotation de l’assemblage au-delà de l’état limite ultime n’a pas été étudiée. Trois niveaux de charge ont été sélectionnés à des fins expérimentales (60, 80 et 100 %) de la valeur d’état limite ultime.
Les valeurs de la rigidité en rotation de l’assemblage semi-rigide ont été obtenues en séparant les effets externes individuels. Le premier facteur externe influençant la rigidité en rotation de l’assemblage était l’assemblage de la partie inférieure des poteaux avec la structure en acier. Un capteur horizontal, S2, a été installé pour obtenir l’inclinaison du poteau à partir de la structure acier, Figure 3.
La deuxième composante était les déformations individuelles des segments de la structure. Leur déformation a pu être calculée à l’aide de la méthode des forces. En soustrayant les composantes de déformation individuelles de la déformation totale obtenue d’un capteur orienté verticalement, S1, Figure 3, nous obtenons la valeur réelle de la déformation causée par la rigidité en rotation de l’assemblage semi-rigide.
ESSAIS EXPÉRIMENTAUX
Les expériences ont été menées dans le Centre d’expérimentation et de diagnostic des bâtiments de l’université technique d’Ostrava (VSB), en République tchèque. La figure 4 (en haut) présente l’expérience A (a) avec la combinaison des boulons et des goupilles, la figure 4 (en bas) présente l’expérience B (b) avec les vis à filetage complet avant la charge statique cyclique. La charge a été appliquée à l’assemblage à l’aide d’un cylindre en acier d’un diamètre de 50 mm. Un bloc en caoutchouc de 10 mm d’épaisseur a été inséré sous ce cylindre pour éviter que le bois ne soit endommagé localement pendant le chargement.
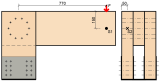
Fig. 3 - Emplacement des capteurs de déformation, vue avant à gauche, vue arrière à droite.


Fig. 4 - Échantillons expérimentaux : expérience A avec la combinaison des boulons et des goupilles (a), expérience B avec les vis à filetage complet (b).
Tableau 1 - Valeurs de résultat de la rigidité en rotation.
|
Méthode |
Type de fixation |
|
Valeur [MNm/rad] |
Comparaison [%] |
|
ČSN EN 1995-1-1 [3] |
Boulons et goupilles |
kr,u,EC5 |
0.323 |
- |
|
kr,u,EC5,1 |
0.299 |
-8 |
||
|
kr,u,EC5,2 |
0.293 |
-10 |
||
|
kr,test,60 |
2.198 |
+85 |
||
|
kr,test,80 |
1.055 |
+31 |
||
|
kr,test,100 |
0.404 |
+20 |
||
|
ČSN EN 1995-1-1 [3] |
Vis à filetage complet |
kr,u,EC5 |
0.323 |
- |
|
kr,u,EC5,1 |
0.206 |
-57 |
||
|
kr,u,EC5,2 |
0.202 |
-60 |
||
|
kr,test,60 |
0.386 |
+16 |
||
|
kr,test,80 |
0.313 |
-3 |
||
|
kr,test,100 |
0.896 |
+64 |
RÉSULTATS DE LA RECHERCHE EXPÉRIMENTALE
Le tableau 1 montre les valeurs tirées de l’expérience. Celles-ci sont comparées aux valeurs de conception obtenues de la norme ČSN EN 1995-1-1 [3]. La valeur pour chaque niveau de charge a été obtenue en faisant la moyenne des valeurs de cinq cycles de charge. Dans cette comparaison, la valeur kr,u,EC5 0,323 MNm/rad est prise en tant que valeur de référence. Cette valeur a été obtenue en substituant les propriétés standard du matériau à la formule de calcul du module de glissement selon la norme susmentionnée. La valeur suivante du tableau est kr,u,EC5,1. Cette valeur a été obtenue en utilisant le diamètre réel mesuré de l’âme de la fixation et la densité réelle mesurée du bois. La dernière valeur de kr,u,EC5,2 est la valeur obtenue au moyen du diamètre réel de l’âme de la fixation et la valeur standard de la densité du bois en fonction de sa classe de résistance.
Les figures 5 et 6 présentent les diagrammes « charge - rigidité en rotation » des assemblages individuels. Cette figure présente également les valeurs de rigidité en rotation calculées pour l’état limite ultime (ELU) et l’état limite ultime sans l’application de facteurs de sécurité partiels (ELU 1).
La figure 7 présente les diagrammes « charge - rigidité en rotation » des fixations individuelles. Le diagramme montre clairement que la rigidité en rotation de l’assemblage présentant des vis augmente légèrement avec l’augmentation des charges, tandis que la rigidité en rotation diminue pour la combinaison de boulons et de goupilles.
La figure 8 présente un modèle numérique de l’angle de structure testé. C’est une composante d’une ossature lourde. L’objectif de ces tests (différents types de fixations ont été utilisés à la fois dans l’angle lui-même et dans les assemblages externes aux éléments en acier) était de déterminer les rigidités en rotation et d’effectuer l’analyse globale du comportement de ce type d’assemblage.
La figure 9 présente des photos des laboratoires de la Faculté de génie civile à l’université technique d’Ostrava (VSB) d’Ostrava.
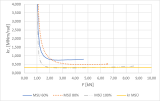
Fig. 5 – Diagramme « Charge - rigidité en rotation », combinaison de boulons et de goupilles.

Fig. 6 – Diagramme « Charge - rigidité en rotation », vis à filetage complet.
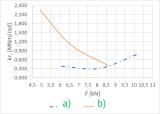
Fig. 7 – Comparaison de la rigidité en rotation des fixations individuelles: (a) vis, (b) boulon

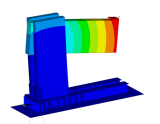
Fig. 8 – Géométrie et maillages d’éléments finis de l’angle de portique (a), déformation totale de la structure analysée (b).


Fig. 9 – Préparation du test d’angle de portique (a), exemple de la déformation de l’angle de portique après la charge (b).
CONCLUSIONS
Les essais expérimentaux d’un assemblage constitué d’une combinaison de boulons et de goupilles couramment utilisée (expérience A) ont prouvé la sécurité et la fiabilité de l’assemblage lorsqu’il est soumis à une charge jusqu’à l’état limite ultime. Du point de vue de la rigidité en rotation, cet assemblage donne, pendant toute la période de chargement, des valeurs plus élevées que celles prévues par la norme pour l’état limite ultime.
Les essais expérimentaux d’un assemblage constitué de vis à filetage complet (expérience B) ont prouvé la sécurité et la fiabilité de l’assemblage lorsqu’il est soumis à une charge jusqu’à l’état limite ultime. Du point de vue de la rigidité en rotation, cet assemblage n’atteint pas des valeurs supérieures à l’hypothèse de la norme pour l’état limite ultime pour le niveau de charge de 80 % de l’ELU. Cette expérience suggère que pour obtenir un résultat plus précis de la rigidité en rotation selon l’Eurocode 5 [3], il est nécessaire d’utiliser le diamètre de la tige de la fixation pour calculer le module de glissement. Il est également possible d’utiliser le diamètre de la tige de l’élément de fixation et la densité du bois mesurée. Étant donné qu’il est difficile, d’un point de vue pratique, d’obtenir la densité de bois mesurée réelle, les données obtenues dans ce document indiquent que la précision suffisante peut être obtenue au moyen du diamètre de la tige de l’élément de fixation et la valeur définie par la norme de la densité du bois.
La question de la détermination de la capacité portante des assemblages en bois selon les normes européennes pour la conception des structures en bois Eurocode 5 [3] est en constante évolution. Cette tendance pourrait également être confirmée par les expériences proposées, qui visaient à déterminer la rigidité en rotation d’un assemblage semi-rigide d’une barre transversale en bois et d’un poteau créé à l’aide de fixations mécaniques de type goupille.
En ce qui concerne la rigidité en rotation, les données des expériences peuvent être utilisées pour la conception pratique de ce type d’assemblage semi-rigide. L’auteur, Marek Johanides, a publié d’autres articles sur la résistance [4], la ductilité [1] et la rigidité en rotation [5] de ce type d’assemblage.
L’avantage du bois est sa capacité de renouvellement et son caractère, que les hommes connaissent et recherchent depuis des millénaires.
Compte tenu de sa densité, la masse de bois présente de très bonnes propriétés de résistance dans le sens longitudinal des fibres. Si l’élément structurel est massif, la résistance au feu est également élevée, et s’il est complété par des éléments de protection passive et active contre le feu, il est possible de construire des maisons en bois à plusieurs étages, comme à Brumunddal, en Norvège.
Le bois, en tant que matériau naturel, est sensible à la décomposition et aux attaques biologiques (champignons et insectes xylophages). Si le bois et ses détails d’assemblage sont suffisamment protégés, ces structures peuvent durer des centaines d’années. (le pont Kapellbrücke, en Suisse)
2. APPLICATION DES POSSIBILITÉS DES MODÈLES NUMÉRIQUES SUR LA CONSTRUCTION RÉALISÉE DU GRAND MAGASIN HUSTOPEČE COOP
OSSATURES LOURDES DANS UNE CONSTRUCTION DURABLE
Les ossatures lourdes en bois sont aujourd’hui une option recherchée pour les bâtiments à plusieurs étages ou les bâtiments lourds. Cette évolution est principalement due à la tendance à rendre l’industrie, dont fait partie le secteur de la construction, aussi durable que possible, en particulier en ce qui concerne les ressources et l’énergie, y compris le respect de l’environnement et les ressources renouvelables. Le bois est un matériau naturel et, en tant que tel, il a ses avantages ainsi que des propriétés qui doivent être améliorées pour atteindre les paramètres requis en fonction du type et de l’objectif du bâtiment.
Avec le développement de la transformation avancée du bois (GLT, CLT, etc.), complété par le développement de détails d’assemblages à haute capacité (acier, résines époxy, fibres de verre et combinaisons de ces matériaux) ainsi que des simulations numériques puissantes complétées par l’expérience normative et les essais physiques, il est désormais possible de concevoir et d’optimiser le bâtiment dans son ensemble, permettant ainsi aux bâtiments à base de bois d’atteindre de nouveaux volumes, de nouvelles formes et de nouvelles silhouettes. La figure 10 présente une visualisation d’une utilisation pratique possible du toit de l’ossature désignée.
L’objectif de cet article est de présenter les possibilités des ossatures lourdes. En général, selon le système statique, les structures porteuses peuvent être divisées en systèmes de portiques, de murs et de treillis. Le système d’ossature est par nature le moins rigide, et cela s’applique encore plus aux assemblages dans les structures en bois. Le système de murs est très rigide et peut être envisagé pour les bâtiments de grande hauteur (noyaux en béton armé des gratte-ciel). Le système de treillis est relativement léger, présente une bonne rigidité et la connexion entre les éléments individuels (avec des forces nodales élevées accumulées ici) est, comme pour les systèmes d’ossatures, également le point dominant. Avec une géométrie appropriée, le système de murs ne conduit pas à des forces nodales aussi élevées dans les assemblages et, par conséquent, ne produit pas de contraintes locales aussi élevées dans les détails d’assemblages. La figure 11 présente la conception d’un hall d’environ 30,6 × 46,3 × 6 m, le plan de sol est essentiellement rectangulaire avec des escaliers latéraux. Le hall est relié à une structure de service latérale des installations.

Fig. 10 – Visualisation non réalisée du grand magasin Hustopeče COOP.
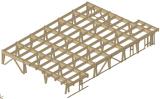

Fig. 11 – Système combiné, schéma de l’ossature lourde – structure et treillis de COOP Hustopeče.

Fig. 12 – Vue de l’entrée du grand magasin.

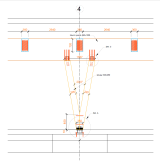
Fig. 13 – Intérieur du grand magasin en fonctionnement (à gauche), détail de l’ancrage du poteau en V (à droite).


Fig. 14 – Vue des éléments d’ossature (à gauche), vis pour le bois et l’acier (à droite).

Fig. 15 – Efforts internes dans les éléments porteurs de la structure.

Fig. 16 – Assemblage de la structure portante principale du hall du grand magasin.
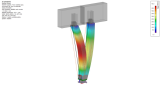

Fig. 17 – Modèle numérique des éléments porteurs de la structure.


Fig. 18 – Efforts internes dans les éléments porteurs de la structure.
GRAND MAGASIN COOP À HUSTOPEČE
Il s’agit d’un centre commercial de plain-pied avec un toit lourd conçu comme un skate park. Le système porteur principal est constitué de poteaux et d’une dalle de toit rigide avec des poutres et des poutrelles. Les éléments en bois sélectionnés sont collés et ont une largeur de 480 mm. La rigidité spatiale de la structure est assurée par des poteaux en A et en V, qui sont disposés dans des grilles rectangulaires avec un plan de toit rigide. Les poteaux sont soumis principalement à des forces de compression et de traction. L’angle de portique est formé par un triangle fermé. La figure 12 présente la structure bardée du hall du grand magasin.
La partie gauche de la figure 13 correspond à la vue de l’intérieur aménagé du grand magasin. On voit ici l’intégration de la structure porteuse dans le schéma nécessaire au fonctionnement du magasin. Malgré son aspect massif, la structure offre une impression naturelle dans l’espace, en mettant l’accent sur le caractère naturel des principaux éléments de la structure du hall. Compte tenu des dimensions des éléments et des connexions cachées, la structure présentera une résistance élevée au feu. La partie droite de la figure 13 présente le poteau, son ancrage et sa connexion à d’autres éléments de la structure du hall.
Figure 14 : sur la partie gauche de la photo, nous pouvons voir les éléments principaux de la structure en Y en bois ; le système d’ossature connecté à la poutrelle. La poutrelle, qui fait 480 × 1 200 mm, est un élément collé composé de bois lamellé-collé de catégorie GL28h. La poutrelle est également connectée aux poutres Gl28h collées avec une section droite de 360 × 720 mm. La poutre est ancrée à la poutrelle au moyen de vis à filetage complet SFS, d’un diamètre de 13 × 500 mm, avec 10 vis par assemblage. L’assemblage est conçu pour un effort tranchant d’environ 211 kN provenant de la charge du toit, y compris les charges climatiques et variables.
L’image de droite montre une fixation mécanique pour le bois et l’acier. Grâce à cette goupille autoperceuse, les éléments en bois peuvent être reliés aux plaques d’acier sans pré-perçage. L’assemblage se caractérise par une capacité de charge et une rigidité élevées. Ces assemblages ont été utilisés dans les têtes et les bases des poteaux.
La figure 16 présente le système porteur principal de l’ossature en bois d’un seul étage avant le bardage. La figure 17 présente ensuite les modèles numériques des éléments porteurs principaux. L’image de gauche représente un mode propre de stabilité sélectionné pour la charge spécifiée. Ce mode propre est déterminé par la flèche locale du poteau. L’image du milieu montre la fixation utilisée (une vis à filetage complet) pour augmenter la capacité de charge du bois dans la compression perpendiculaire au grain, pour transmettre les efforts tranchants (voir la figure 15) et pour encastrer la masse de bois dans une traction perpendiculaire au grain. L’image de droite montre une structure porteuse de type « A » avec un comportement de treillis.
Cette image montre comment le système d’éléments en bois et en acier est modélisé numériquement. Le modèle numérique est composé d’éléments de coque et de poutre [7], tenant compte de la fondation et de la non-linéarité physique et géométrique. En outre, le glissement dans les assemblages et la non-linéarité structurelle avec les imperfections sont également pris en compte. Un tel modèle peut être analysé séparément ou dans le cadre d’un modèle global. Si le modèle séparé est intégré au modèle numérique global, la complexité de la solution augmente. Toutefois, l’interaction est plus réaliste parce que les conditions annexes sont fournies par la modélisation « réelle » de l’assemblage des éléments individuels.
La figure 18 présente un détail de la structure de gauche issue de la figure 17, à savoir sa plaque d’embase. L’image de gauche montre la contrainte de contact entre l’étrier en acier et la base en béton armé. La contrainte de contact ici correspond environ à 10,20 MPa pour une force de compression d’environ 1 144 kN. L’image de droite montre le mode propre de stabilité pour la charge qui doit générer la compression maximale. Le flambement local de l’âme la plus longue du caisson fermé en acier est clairement visible. Les modes propres mentionnés ici correspondent à environ 2,7 fois la charge saisie. L’avantage des modèles numériques complexes est que le calcul des modes de stabilité non linéaire prend en compte la rigidité globale.
La figure 19 montre une partie du système porteur de l’ossature bois sélectionnée dans l’ensemble du modèle numérique. Ce modèle numérique est composé d’éléments finis de volume et de poutre. Le problème est un problème de contact, et il prend en compte l’orthotropie du bois avec des diagrammes bilinéaires contrainte-déformation pour le bois et l’acier.
La partie gauche de la figure 20 montre le maillage d’éléments finis de la poutrelle et la poutre avec les vis en acier. L’assemblage se fait par l’intermédiaire de contacts avec frottement et glissement. Le modèle numérique illustré dans la figure fait partie du modèle global, voir la figure 19. L’emplacement du maillage du détail analysé de l’assemblage en cisaillement a été choisi de manière à ce que l’assemblage soit soumis à environ 211 kN, ce qui correspond à la force maximale dans le modèle de poutre. L’image de droite est un détail des vis qui sont installées dans la poutrelle et les poutres et qui forment un assemblage en cisaillement.
L’image montre une contrainte atteignant environ 1 019 MPa dans la zone de l’assemblage de la poutre et de la poutrelle. Cette partie de l’assemblage se comporte comme un treillis, ce qui correspond aux hypothèses appliquées dans la conception de cet assemblage. Cet assemblage est utilisé dans la pratique de la construction depuis des décennies.
Figure 21 : la partie gauche montre la contrainte de cisaillement dans l’élément de poutrelle avec une dimension de 480 × 1 200 mm. La contrainte de cisaillement dans l’assemblage de la poutre et de la poutrelle atteint une valeur d’environ 2 MPa. Pour le bois plein et ce type et cette direction de charge, la norme prescrit la valeur caractéristique de contrainte de 2,7 MPa. La valeur de la résistance au cisaillement pour la charge mentionnée est comprise entre 3 MPa et 6 MPa. L’image de droite montre une contrainte dans la poutre de 360 × 720 mm. Le comportement est similaire au comportement illustré dans l’image de gauche pour la poutrelle. L’analyse a également pris en compte les imprécisions possibles dans l’assemblage de contact entre la poutrelle et la poutre. Les variantes des modèles numériques ont pris en compte à la fois le contact immédiat entre la poutrelle et la poutre, et un espace qui restera entre les éléments de la poutre et la poutrelle même après la charge.
Les modèles analysés ont révélé que l’influence du contact entre la face de la poutre et la surface de la poutrelle n’a pas d’effet significatif sur la contrainte dans les vis jusqu’à environ 7 % de la contrainte de Von Mises. Lorsque la poutre et la poutrelle sont en contact total, on observe une augmentation notable de la contrainte de contact perpendiculaire au grain, qui peut atteindre localement 5,0 MPa.
La figure 22 illustre la distribution des contraintes perpendiculaires au grain. Pour la charge à l’extrémité de la poutre de 211 kN, le maximum local de la contrainte de traction perpendiculaire au grain est de 2,70 MPa et le minimum local de la contrainte de compression perpendiculaire au grain est de 5 MPa. Ce sont des valeurs à la limite de la résistance du bois. En raison de leur nature, il s’agit en partie d’un problème numérique extrême causé par des simplifications dans la modélisation et par le choix d’un modèle de matériau qui ne peut pas décrire complètement le comportement (anisotropie) du bois. En principe, ces extrêmes apparaissent et s’accumulent dans la zone où les vis se croisent et passent de la poutre à la poutrelle. La contrainte inférieure dans la poutrelle perpendiculaire au grain est donnée par le modèle numérique, qui prend en compte le contact instantané entre la poutre et la poutrelle et son enfoncement dans la poutrelle autour de son bord inférieur. Ici, en raison du frottement, la charge des vis change également légèrement, parce qu’elles sont contraintes de pivoter autour d’un point spécifique. Figure 22 : la partie de droite illustre la déformation des poutres et de la poutrelle. La valeur minimale est d’environ 9 mm et la valeur maximale est de 12 mm. Le glissement mutuel entre la face de la poutre et la projection de la face de la poutre sur la poutrelle causé par l’effort tranchant maximal de 211 kN par assemblage est d’environ 0,977 mm.
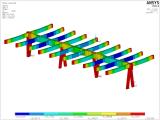
Fig. 19 – Déformation d’une poutrelle sélectionnée y compris le détail de l’assemblage en cisaillement, modèle ANSYS [6].

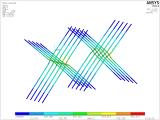
Fig. 20 – Détail du modèle numérique du maillage d’éléments finis et des vis.
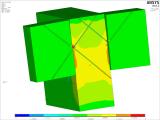
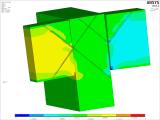
Fig. 21 – Contrainte de cisaillement dans la poutrelle et la poutre dans le détail d’assemblage sélectionné.
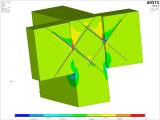
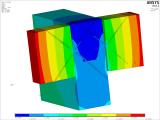
Fig. 22 – Détail du modèle numérique, contrainte de traction perpendiculaire au grain et déformation de l’assemblage.
APPLICATION DES MÉTHODES NUMÉRIQUES DANS LA PRATIQUE
Pour résumer l’analyse des ossatures lourdes et de leurs détails, l’application de méthodes numériques est avantageuse pour les détails et les structures qui sont nouveaux dans leur nature ou qui sont soumis à des charges élevées et dont la géométrie et la méthode d’ancrage sont moins connues. Les méthodes numériques doivent être complétées par une méthode de résolution définie par la norme, par la littérature professionnelle et, si nécessaire, par des essais physiques. Les consultations avec des experts chevronnés dans le domaine constituent également un élément essentiel.
Lorsque cette gamme d’approches pour résoudre de nouveaux types d’assemblages et de structures est disponible, il est possible d’assembler des structures complexes et d’optimiser leur système et leurs détails afin que leur résistance et leur rigidité soient accompagnées d’une réponse appropriée en termes de ductilité.
À l’heure actuelle, lorsqu’il est approprié et nécessaire de prendre en compte l’état de la planète et ses ressources, sans lesquelles notre civilisation n’est pas en mesure de survivre sous sa forme actuelle, le développement dans le champ de bâtiments à base de bois peut amener des matériaux écologiques et dégradables qui sont non seulement beaux, mais également fonctionnels et capables de supporter des charges élevées. De cette manière, un large secteur de la construction peut en bénéficier, de la construction familiale aux complexes immobiliers en passant par les immeubles de grande hauteur (par exemple, en Scandinavie, en Autriche et en Angleterre).
BIBLIOGRAPHIE
[1] Johanides, M.; Lokaj, A.; Mikolasek, D.; Mynarcik, P.; Dobes, P.; Sucharda, O. Timber Semirigid Frame Connection with Improved Deformation Capacity and Ductility. Buildings 2022, 12, 583. https://doi. org/10.3390/buildings12050583.
[2] Timber Structures According To Eurocode 5; STEP 1: Design and construction materials ; traduit par Bohumil Koželouh ; KODR: Zlín, République tchèque, 1998 ; ISBN 80-238-2620-4 (en tchèque).
[3] ČSN EN 1995-1-1. Eurocode 5 : Conception des structures en bois – Partie 1-1 : Généralités – Règles communes et règles pour les bâtiments ; Institut des normes tchèques : Prague, République tchèque, 2006.
[4] Johanides, M.; Lokaj, A.; Dobeš, P.; Mikolášek, D. Numerical and Experimental Analysis of the Load-Carrying Capacity of a Timber Semi-Rigid Dowel-Type Connection. Materials 2022, 15, 7222. https://doi.org/10.3390/ma15207222.
[5] Johanides, M.; Lokaj, A.; Dobeš, P.; Mikolášek, D. Numerical and Experimental Analysis of the Rotational Stiffness of a Timber Semi-Rigid Dowel-Type Connection. Materials 2022, 15, 5622. https://doi.org/10.3390/ma15165622.
[6] ANSYSTM, disponible sur www.ansys.com.
[7] SCIA Engineer, disponible sur www.scia.net.
Auteurs :
Ing. Marek Johanides, Ph.D., est spécialisé dans les structures en bois et en acier en ce qui concerne la modélisation numérique complétée par des essais physiques. Il est membre du Centre d’expérimentation et de diagnostic des bâtiments de l’université technique d’Ostrava (VSB), en République tchèque.
Prof. Ing. Antonín Lokaj, Ph.D., est spécialisé dans les structures en bois et en acier en ce qui concerne la recherche appliquée et le développement des détails d’assemblage dans les structures combinées. Il est le chef du département des structures et vice-doyen pour le développement à la Faculté de génie civil, à l’université technique d’Ostrava (VSB), en République tchèque.
Ing. David Mikolášek, Ph.D., est spécialisé dans les structures en bois, en acier et composites en ce qui concerne la modélisation numérique validée par des essais physiques. Il est membre du département des structures à la Faculté de génie civil, à l’université technique d’Ostrava (VSB), en République tchèque.
Ing. Pavel Dobeš, Ph.D., est spécialisé dans les structures de construction et les détails en ce qui concerne les diagnostics, les tests et les calculs. Il est membre du Centre d’expérimentation et de diagnostic des bâtiments de l’université technique d’Ostrava (VSB), en République tchèque.
Ing. Pavel Vlček, Ph.D., est spécialisé dans le domaine de la construction civile et l’inclusion de nouvelles connaissances sur les systèmes structurels dans la pratique de la construction. Il est membre du département de génie civil à la Faculté de génie civil, à l’université technique d’Ostrava (VSB), en République tchèque.
Ing. Robert Martinek est un spécialiste des structures en bois qui se concentre sur la conception, l’optimisation et la production de détails et de structures en bois. Il travaille en tant que directeur exécutif chez EXTEN CZ.
Cet article a été publié dans le magazine KONSTRUKCE 4/2023 (https://konstrukce.cz).