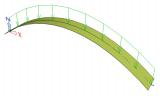
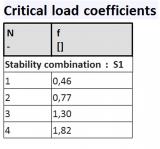
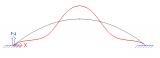
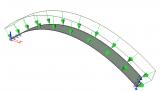
sens.01 - Stabiliteitsanalyse (SCIA Engineer)

Home
SCIA Engineer
Fact sheets
Analyse resultaten
sens.01 - Stabiliteitsanalyse

Modulecode sens.01
Software
- SCIA Engineer
Inbegrepen in edities
- Concept,
- Professional,
- Expert,
- Ultimate
Categorie Analyse en resultaten
Licentie Permanent

Belangrijkste kenmerken

Invoeren van het aantal te berekenen knikmodi.
De berekende knikfactoren (verhoudingen tussen de kritieke knikbelasting en de toegepaste belasting) zijn onderdeel van het resultaat.
Vanr elke berekende knikmodus kunnen vervormingen grafisch worden weergegeven.
De kritieke knikmodus kan worden geïmporteerd in de geometrische niet-lineaire berekening als een oorspronkelijke vervorming (in combinatie met de geometrische niet-lineaire module).

Deze module berekent de algemene knikmodus (eigenmodus) van een structuur onder de gegeven belasting. Daarnaast wordt de verhouding tussen de knikbelasting en de toegepaste belasting gegeven. Stabiliteitsberekeningen worden gebruikt om inzicht te krijgen in de knikmechanismen van een structuur, om de kniklengte van een element te berekenen dat in de staalnormcontrole wordt gebruikt en om te controleren of tweede-ordeberekeningen nodig zijn. Deze module helpt bij het bepalen van de algemene kritieke knikmodus en de knikbelasting van raamwerkstructuren en de oppervlakte-elementen (platen en schalen) daarvan.

Het principe van superpositie is niet geldig voor een stabiliteitsberekening. De combinaties moeten voorafgaand aan de berekening worden samengesteld. In SCIA Engineer wordt dit gedaan door stabiliteitscombinaties te definiëren. Een stabiliteitscombinatie wordt gedefinieerd als een lijst belastingsgevallen waarbij elk belastingsgeval een bepaalde coëfficiënt heeft. Net zoals is aangegeven voor niet-lineaire combinaties, kunnen de lineaire combinaties worden geïmporteerd als stabiliteitscombinaties.

De volgende aannames worden gemaakt in de berekening:

Er is sprake van fysieke lineariteit
De elementen worden beschouwd als ideaal recht en zonder onvolkomenheden.
De belastingen worden door de netknooppunten geleid, waardoor het net met de eindige elementen moet worden verfijnd om precieze resultaten te behalen.
De belasting is statisch.
De kritieke belastingscoëfficiënt is per modus dezelfde als voor de structuur als geheel.
Tussen de netknooppunten worden de normaalkrachten en momenten als constant beschouwd.

Opmerkingen

De eerste eigenmodus is meestal de belangrijkste en correspondeert met de laagste kritieke belastingscoëfficiënt. Een mogelijke instorting van de structuur treedt meestal op in deze eerste modus.
De structuur wordt instabiel voor de gekozen combinatie als de belasting een waarde bereikt die gelijk is aan de huidige belasting vermenigvuldigd met de kritieke belastingsfactor.
Een kritieke belastingsfactor die kleiner is dan 1 geeft aan dat de structuur instabiel is voor de gegeven belasting.
Aangezien de berekening waarden zoekt die bijna nul bedragen, kunnen de berekende I-waarden zowel positief als negatief zijn. Een negatieve kritieke belastingsfactor geeft een trekbelasting aan. De belasting moet dus worden omgekeerd wil knik optreden (wat bijvoorbeeld het geval kan zijn bij windbelastingen).
De eigenmodi (knikvormen) zijn dimensieloos. Alleen de relatieve waarden van de vervormingen zijn van belang, de absolute waarden hebben geen betekenis.
Voor schaalelementen wordt slechts in één richting geen rekening gehouden met de normaalkracht. De schaalelementen kunnen in één richting onder dril staan en tegelijkertijd in de tegenoverliggende richting onder spanning staan. Zodoende kan het element in de ene richting knikken en in de andere richting verstijven. Dit is de reden voor de aanzienlijke postkritieke draagcapaciteit van dergelijke structuren.
Initiële spanning is de enige plaatselijke niet-lineariteit waarmee in een lineaire stabiliteitsberekening rekening wordt gehouden.
Vergeet niet dat een stabiliteitsberekening uitsluitend het theoretische knikgedrag van een structuur onderzoekt. Het is dus nog altijd noodzakelijk dat een staalnormcontrole wordt uitgevoerd om rekening te houden met kip, doorsnedecontroles, gecombineerde normaalkracht en buiging.