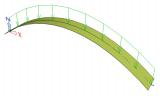
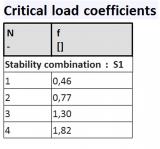
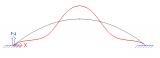
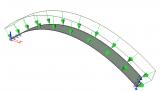
sens.01 - Stabilitätsanalyse
- Modulcode sens.01
-
Software
- SCIA Engineer
-
Eingeschlossen in den Editionen
- Concept,
- Professional,
- Expert,
- Ultimate
- Kategorie Berechnung & Ergebnisse
- Lizenz Unbefristet