Deformační zatížení
Typy zatížení dostupné v projektu závisí na typu projektu (2D, 3D apod.) a na nastavené funkcionalitě. Počet možných typů zatížení je veliký. V tomto článku probereme předepsané deformace určitého místa na konstrukci.
Přemístění uzlu - Posun podpory
Uzel konstrukce může být zatížen předepsaným přemístěním. V takovém případě uživatel definuje směr a velikost známého přemístění.
Parametry jsou tyto:
-
Jméno: jméno použité pro identifikaci entity.
-
Směr: určuje směr, ve kterém podpora „sedne“.
- Reference:
→ Absolutně: Hodnota (viz dále) se zadá absolutní hodnotou vztaženou k počátku globálního souřadného systému.
→ Relativně: Hodnota (viz dále) se zadá relativní hodnotou vztaženou k poloze podpory.
-
Hodnota U: definuje hodnotu, o kterou se podpora posune.
-
Systém: směr je vždy definován v lokálním souřadném systému podpory (informativní).

Posun podpory lze zadávat POUZE u pevných podpor. Není možno jej použít u pružných a nelineárních podpor.
Příklad
Příklad demonstruje rozdíl mezi absolutní a relativní referencí.
Předpokládejme jednoduchý rám o třech polích s podporami podle obrázku.

Máme dva shodné rámy, na levém je zadán absolutní posun podpory, na pravém relativní posun. Globální souřadnice Z spodní podpory je rovna nule, tj. podpory jsou umístěny v globální rovině XY.
Posun je předepsán podpoře uprostřed rozpětí středního pole.
Na levém rámu je posun zadán následovně:
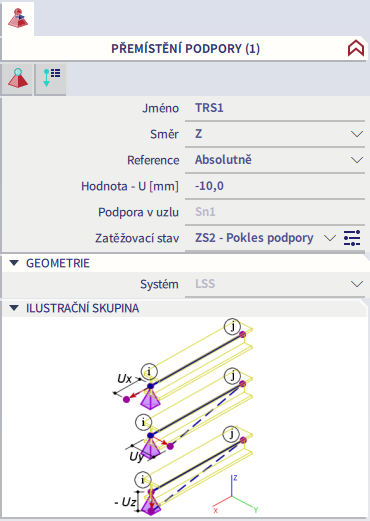
Na pravém pak takto:
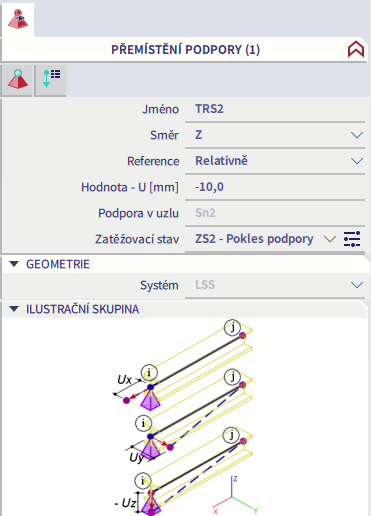
Rozdíl mezi absolutní a relativní referencí je zřejmý z posledního obrázku (výška rámu je 4 metry).

Posun bodu na prutu - Relativní přemístění na 1D
Bod na konstrukci může být zatížen předepsaným přemístěním. Přemístění znamená, že 1D dílec je v zadaném bodě „roztržen“ a jedna část dílce je zvednuta nahoru a druhá je stlačena dolů. Vnesené zatížení je zřejmé z přiloženého obrázku. Zadaná velikost je rovna vzdálenosti „odtržených“ konců dílce.


Rotace uzlu - Natočení podpory
Uzel konstrukce může být zatížen předepsaným pootočením. V takovém případě uživatel definuje směr a velikost známého pootočení.

Poznámka: Pootočení podpory nelze definovat u pružných a nelineárních podpor.
Natočení bodu na prutu - Relativní pootočení na 1D
Bod na konstrukci může být zatížen předepsaným pootočením. Pootočení znamená, že dílec je v daném bodě „zlomen“ a obě části jsou ohnuty. Vnesené zatížení je zřejmé z přiloženého obrázku. Zadaná velikost je rovna úhlu tečen vedených v koncovém bodě na jednotlivých částech „zlomeného“ dílce.


Podélné přetvoření na 1D - podélné namáhání
Celý 1D prut může být vystaven podélnému namáhání. Tato deformace může být buď rovnoměrná podél nosníku, nebo se může lineárně měnit.
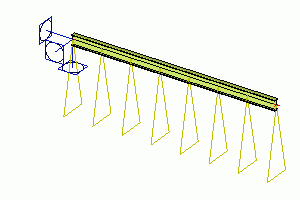
Ohybové přetvoření na 1D - ohybové napětí
Celý 1D prut může být namáhán ohybem. Tato deformace může být buď rovnoměrná podél nosníku, nebo se může lineárně měnit.
Parametry mají následující význam:
- Jméno: slouží k identifikaci zatížení.
- Směr: určuje základní směr zatížení. Směr může být dále specifikován vlastnostmi 1D prvku "Pootočení LSS" a "Alfa".
- Rozložení: zatížení může být buď konstantní podél 1D prutu, nebo lineárně proměnné (lichoběžníkové).
- Hodnota R: určuje velikost zatížení.
- Systém: určuje souřadnicový systém, ke kterému je zatížení aplikováno. Pro tento typ zatížení je možné použít pouze LSS.
- Poloha: určuje, zda je zatížení zadáno přímo na délku šikmého 1D prutu, nebo zda je zatížení zadáno na průmět půdorysu (zde je k dispozici pouze možnost délky).
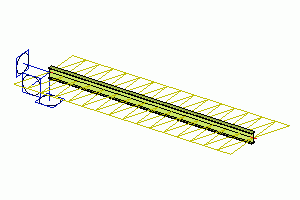
Osové a ohybové přetvoření na 2D
Parametry:
- Jméno: určuje název zatížení. Může usnadnit identifikaci zatížení.
- Epsilon [mm/m']: relativní prodloužení/zkrácení v důsledku zvýšení teploty nebo smrštění.
- k [mrad/m']: zakřivení roviny v důsledku nerovnoměrného zvýšení teploty nebo smrštění.
Uvážíme-li, že materiál je homogenní a izotropní a že teplota je rozložena lineárně po tloušťce 2D prvku, tak je možné snadno vypočítat prodloužení prvku v důsledku zvýšení teploty.
Předpokládejme zvýšení teploty na horním povrchu TH a zvýšení teploty na dolním povrchu TD. Konečné zvýšení teploty (smrštění) lze rozdělit na dvě složky - viz obrázek níže.

S ohledem na to dostaneme hodnoty:
- přetvoření (v m/m'):
alfa: koeficient teplotní roztažnosti
Ts: zvýšená teplota
Kladné zvýšení teploty dává kladnou hodnotu přetvoření.
- zakřivení:
alfa: koeficient teplotní roztažnosti
delta T: rozdíl teplot mezi povrchem z = -h/2 a z = +h/2.
h: tloušťka prutu
Z geometrie vyplývá, že k = 1 / R, kde R je poloměr kulové plochy, jejíž tvar prvky zaujímají, pokud není zabráněno změně tvaru v důsledku zvýšení teploty.
Poznámka: Pokud není nárůst teploty napříč prvkem lineární, je třeba rozložení nárůstu teploty linearizovat. Výsledky se pak musí revidovat a napětí vyplývající z rozdílu mezi daným a linearizovaným nárůstem teploty se musí získat zvláštním výpočtem a přičíst k tomuto výsledku.
Představme si následující - spíše teoretickou - situaci. Mějme kruhovou desku podepřenou pouze v jejím středu.
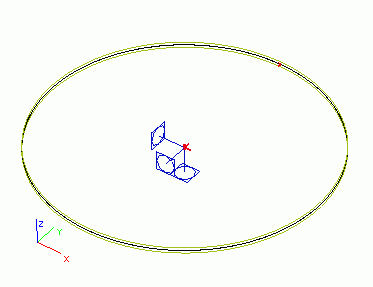
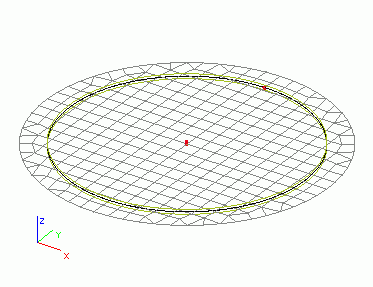
Nejprve tuto desku zatížíme rovnoměrným prodloužením 10 mm/m. Lze si představit, že oba povrchy desky jsou zahřáté.
Po výpočtu můžeme vidět celkové a symetrické roztažení desky (na obrázku je zobrazena jak původní deska, tak deformovaná síť konečných prvků).
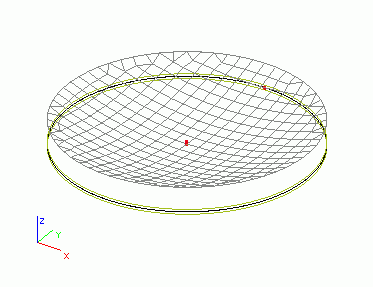
Ve druhém případě je deska zatížena nerovnoměrným přetvořením (zakřivení) o velikosti 10 mrad/m. Je možné si představit, že se ohřívá pouze jeden povrch desky.
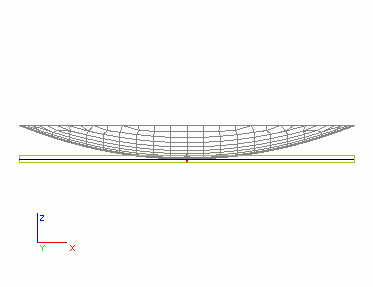
Po výpočtu můžeme vidět miskovitou deformaci desky, která je výsledkem tohoto typu zatížení. Na obrázku je zobrazena jak původní deska, tak deformovaná síť konečných prvků. Na druhém obrázku je deska z bočního pohledu - tento obrázek je názornější.