Charges de déplacement

​

Les types de charge disponibles dans un projet particulier peuvent dépendre du type de projet (2D, 3D, etc.) et de la fonctionnalité ajustée pour le projet. Le nombre de types de charge disponibles est vraiment important. Dans cet article, nous présentons l’effet des déplacements prescrits pour des points spécifiques de la structure.

Déplacement de point - Traduction du support

Un nœud de la structure peut être soumis à un déplacement prescrit. Dans un tel cas, l’utilisateur définit la direction et l’ampleur du déplacement connu.

 

Les paramètres ont la signification suivante :

• Nom
  Le nom est utilisé pour l’identification de l’entité.
• Direction
  La direction spécifie la direction dans laquelle le support « se dépose ».
• Valeur absolue de référence
  : la valeur (ci-dessous) est entrée en valeur absolue liée à l’origine du repère global.
  Relative : La valeur (ci-dessous) est entrée en valeur relative liée à la position du support.
• Valeur - U
  Spécifie la valeur par laquelle le support est traduit.
• Système
  La direction est toujours définie dans le système de coordonnées local du support (informatif).

La traduction du support ne peut être définie QUE dans les supports fixes ; il ne peut pas être défini dans des supports flexibles et non linéaires.

Cet exemple illustre la différence entre la référence absolue et la référence relative.
Supposons un cadre simple à trois travées avec des supports comme indiqué sur l’image.

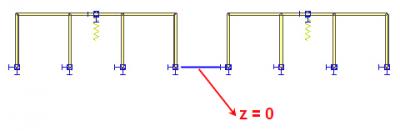
Nous avons deux cadres identiques : celui de gauche pour la traduction absolue du support, le droit pour la traduction relative. La coordonnée Z globale des supports inférieurs est égale à zéro, c’est-à-dire que les supports sont situés dans le plan XY global.
La translation d’un support est affectée au support situé au milieu de la poutre de portée centrale.

Le déplacement dans le cadre de gauche est entrée avec les valeurs suivantes :

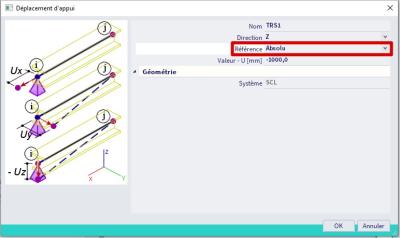
La bonne variante avec les paramètres suivants :

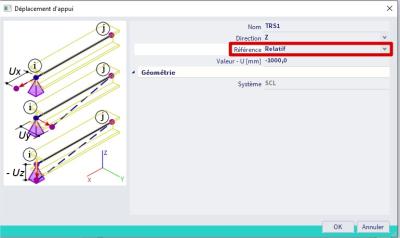
La différence entre la référence absolue et la référence relative peut être clairement vue dans la dernière image (la hauteur du cadre est de 4 mètres).

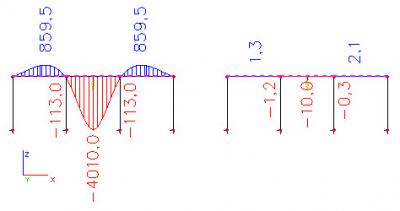
Déplacement de point - Translation d’un point sur faisceau - rel. traduction

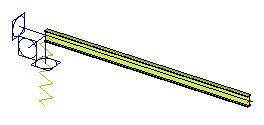
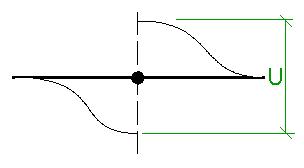
Un point de la structure peut être soumis à un déplacement prescrit. Le déplacement signifie que l’élément 1D est « déchiré » et qu’une partie de l’élément 1D est soulevée tandis que l’autre partie est poussée vers le bas. La charge imposée est claire sur l’image ci-dessous. La magnitude définie est égale à la distance des « points d’extrémité déchirés » de l’élément 1D.

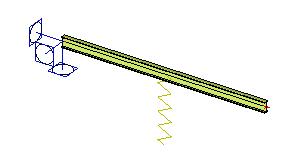
Déplacement de point - Rotation du support

Un nœud de la structure peut être soumis à une rotation prescrite. Dans un tel cas, l’utilisateur définit la direction et l’ampleur de la rotation connue.

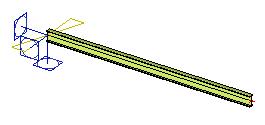
Remarque : La rotation du support ne peut pas être définie dans les supports flexibles et non linéaires.

Déplacement de point - Rotation d’un point sur poutre

Un point de la structure peut être soumis à une rotation prescrite. La rotation signifie que l’élément 1D est « fissuré » et que les deux parties sont pliées. La charge imposée est claire sur l’image ci-dessous. La magnitude définie est égale à l’angle entre les tangentes et les deux parties de l’élément 1D.

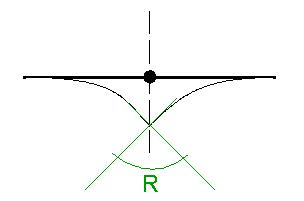
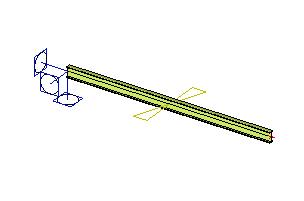
Déplacement de la ligne sur le faisceau - déformation longitudinale

L’ensemble de l’élément 1D peut être soumis à une déformation longitudinale. Cette déformation peut être uniforme le long de l’élément ou varier linéairement.

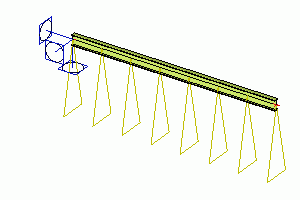
Déplacement de ligne sur poutre - déformation flexionnelle

L’ensemble de l’élément 1D peut être soumis à une déformation de flexion. Cette déformation peut être uniforme le long de l’élément ou varier linéairement.

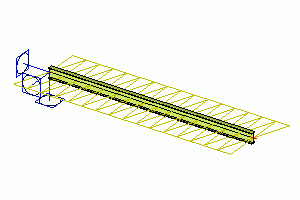
Les paramètres ont la signification suivante

• Nom: est utilisé pour l’identification de la charge
• Direction : spécifie la direction de base de la charge. la direction peut en outre être spécifiée par le paramètre « angle »
• Distribution : la charge peut être soit constante le long de l’élément 1D, soit linéairement variable (trapézoïdale)
• Valeur R : spécifie la taille de la charge
• Système : définit le système de coordonnées dans lequel la charge est appliquée. Seul LCS est possible pour ce type de charge
• Emplacement : spécifie si la charge est « placée directement sur un élément 1D incliné » ou si la « projection sur plan » est définie (seule l’option longueur est disponible ici)

Déplacement des éléments 2D, courbure

Paramètres:

• Nom : définit le nom de la charge. Il peut faciliter l’identification de la charge.
• Epsilon [mm/m']: allongement relatif dû à l’augmentation de la température ou au retrait.
• k [m_rad/m']: courbure du plan due à une augmentation non uniforme de la température ou du retrait.

Étant donné que le matériau est homogène et isotrope et que la température est répartie linéairement sur l’épaisseur de l’élément, l’allongement d’un élément dû à l’augmentation de la température peut être facilement calculé.

Supposons une augmentation de la température à la surface supérieure TH et une augmentation de la température à la surface inférieure TD. L’augmentation finale de la température (retrait) peut être divisée en deux composantes – voir la figure ci-dessous.

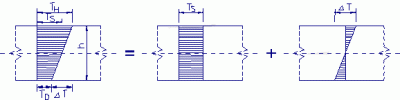
Compte tenu de cela, nous obtenons:

• allongement (en m/m'):

alpha: coefficient de dilatation thermique
Ts: l’augmentation de la température
L’augmentation positive de la température donne une valeur positive d’allongement.

• courbure:

alpha: coefficient de dilatation
thermique delta T: différence de température entre la surface z = -h/2 et z = +h/2.
h: épaisseur des membres
Il résulte de la géométrie que k = 1 / R, où R est un rayon d’une surface sphérique dont les membres prennent la forme si le changement de forme dû à une augmentation de la température n’est pas empêché.

Remarque: Si l’augmentation de la température n’est pas linéaire à travers l’élément, la distribution de l’augmentation de la température doit être linéarisée. Les résultats doivent ensuite être révisés et la contrainte résultant de la différence entre l’augmentation donnée et linéarisée de la température doit être obtenue par un calcul spécial et ajoutée à ce résultat.

Imaginez la situation suivante – plutôt théorique . Ayons une dalle circulaire soutenue en son centre seulement.

Tout d’abord, soumettons cette dalle à l’allongement uniforme de 10 mm/m. Il est possible d’imaginer que les deux surfaces de la dalle sont chauffées.

Après calcul, nous pouvons voir l’expansion globale et symétrique de la dalle (la figure montre à la fois la dalle d’origine et le maillage d’éléments finis déformé).

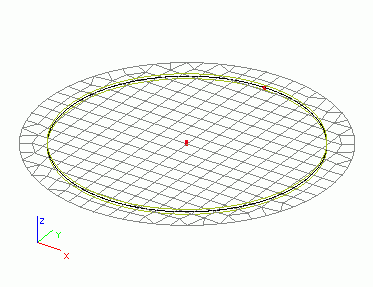
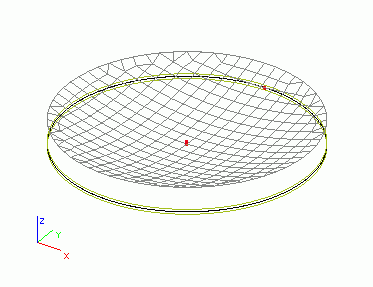
Deuxièmement, soumettons la dalle à une expansion non uniforme (courbure) de 10 mrad/m. Il est possible d’imaginer qu’une seule surface de la dalle est chauffée.

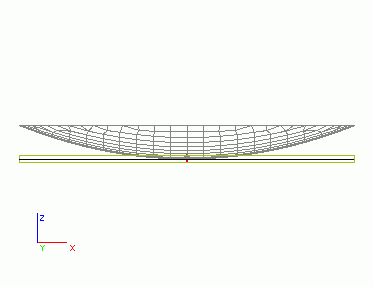
Après calcul, nous pouvons voir la déformation en forme de bol de la dalle qui résulte de ce type de charge. La figure montre à la fois la dalle d’origine et le maillage d’éléments finis déformé. La deuxième figure présentant la vue latérale est plus illustrative.

​