scia.a.geo_nl - Geometrische Nichtlinearität

Mit diesem Modul können Sie Berechnungen nach zweiter Ordnung durchführen. Diese ermöglichen die Berechnung der Struktur im verformten Zustand unter Berücksichtigung des P-Delta-Effekts (anfängliche Verschiebungen und Elementimperfektionen) sowie des Einflusses der Normalkräfte auf die Steifigkeit.

Eine Analyse zweiter Ordnung kann an einer ursprünglich verformten Struktur durchgeführt werden, wobei geometrische Imperfektionen (Anfangsverformungen und Elementimperfektionen) berücksichtigt werden:

• Lokale Krümmungsimperfektion, die vom Benutzer oder nach Eurocode festgelegt wird
• Gesamtimperfektion vom Anwender vorgegeben oder nach Eurocode
• Allgemeine Knickform aus Stabilitätsanalyse

 

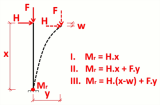
Analyse 1. Ordnung

Das ist die lineare Standardberechnung. Sie darf nur verwendet werden, wenn die Auswirkungen der Verschiebung auf das Verhalten der Struktur vernachlässigbar sind.

Analyse 2. Ordnung: Timoschenko-Methode

Diese Methode basiert auf der exakten Timoshenko-Lösung für Stäbe mit bekannter Normalkraft. Es handelt sich um eine Theorie 2. Ordnung mit Gleichgewicht an der verformten Struktur, die von kleinen Verschiebungen, kleinen Drehungen und kleinen Dehnungen ausgeht. Der Einfluss der Normalkraft auf die Biegesteifigkeit und die zusätzlichen Momente, die durch die Querverschiebungen der Struktur verursacht werden (der P-Δ-Effekt), werden bei dieser Methode berücksichtigt. Die Methode benötigt nur zwei Iterationsschritte, was zu einer großen Effizienz führt. Im ersten Schritt werden die Axialkräfte gelöst. Im zweiten Schritt werden die ermittelten Normalkräfte für die exakte Lösung von Timoshenko verwendet. Als Standard-Iterationsmethode ist die Picard-Methode eingestellt. Diese ist für die meisten Fälle von nichtlinearem Verhalten von Gebäuden geeignet und wird als Standard für geometrische Nichtlinearität eingestellt.

 Analyse 2. Ordnung: Newton-Raphson-Methode

Sie wird auch als "Analyse großer Verformungen" bezeichnet und basiert auf der Newton-Raphson-Methode zur Lösung nichtlinearer Gleichungen. Es handelt sich um eine allgemeinere Methode, die für die meisten Problemtypen sehr zuverlässig ist. Sie kann für sehr große Verformungen und Verdrehungen verwendet werden, eignet sich aber auch für kleine Verschiebungen und kleine Dehnungen. Mathematisch basiert die Methode auf einer schrittweisen Erhöhung der Belastung. Diese Art der iterativen Lösung eignet sich vor allem für Modelle mit Membranen und Seilen wie zum Beispiel Brücken.