Schwindeffekte in der nichtlinearen Analyse

Bei der Planung von Betonkonstruktionen reicht eine lineare Analyse in der Regel nicht aus. Es gibt mehrere andere Aspekte, die das Verhalten der Struktur beeinflussen, vorrangig unter dem Gesichtspunkt der Gebrauchstauglichkeit. Diese Effekte sind hauptsächlich:

• Betonrisse
• Kriechen und Schwinden

Das Reißen von Beton ist in der Regel ein irreversibler Effekt, der auftritt, wenn die Zugfestigkeit des Betons überschritten wird. Die Struktur kann jedoch auch mit Rissen noch haltbar und zuverlässig sein, wenn diese unterhalb der in den Normen festgelegten Grenzen liegen. In diesem Artikel geht es hauptsächlich um diese Effekte während der Planung mit Schwerpunkt auf Schwinden.

Schwindeffekt

Kriech- und Schwindphänomene sind die wichtigsten zeitabhängigen Materialeigenschaften von Beton. Wenn Beton vor Ort eingebracht wird, beginnt der Zement unter Verwendung des freien Wassers in der Mischung zu hydratisieren. In der Regel tritt das Wasser aus dem Beton aus und der Prozess des Trocknungsschwindens beginnt. Aus diesem Grund muss der Beton insbesondere in den ersten Phasen nach dem Gießen ausgehärtet werden. Ohne einen speziellen Aushärtungsprozess entstehen im Beton zusätzliche Spannungen, die zu Schwindrissen führen können.
Der zweite Teil des Schwindens ist das autogene Schwinden, bei dem der Beton während des Aushärtungsprozesses sein eigenes Wasser verbraucht. Die Größe des autogenen Schwindens hängt hauptsächlich vom Wasser-Zement-Wert (w/z) ab. Je niedriger der w/z-Wert, desto größer das autogene Schwinden.
Es gibt mehrere Aspekte, die den Fortschritt des Schwindens beeinflussen:

• Beginn und Dauer der Aushärtung
• Menge und Position der Bewehrung
• Abmessungen der Struktur
• Relative Luftfeuchtigkeit und Temperatur
• Zementart
• Und andere

Theoretischer Hintergrund

Wie oben erwähnt, setzt sich das Gesamtschwinden (ε_cs(t,ts)) aus zwei Teilen zusammen:

• Trocknungsschwinden (ε_cd(t,ts))
• Autogenes Schwinden (ε_ca(t))

ε_cs(t,ts) = ε_cd(t,ts) + ε_ca(t)

Die Berechnung beider Dehnungen wird direkt in EN1992-1-1[1] beschrieben.
SCIA Engineer [2] berücksichtigt standardmäßig automatisch beide Teile der Schwindverformung. (Dies kann bei Bedarf in den Betoneinstellungen/Betonbauteildaten deaktiviert werden). Der Wert der Schwindverformung wird auf Grundlage der vordefinierten Aushärtezeit und der Belastungszeit berechnet.

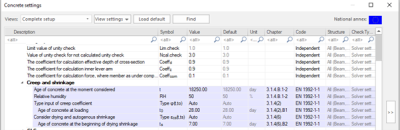
Die durch Schwinden verursachten Verformungen werden auf der Grundlage der durch das Schwinden verursachten Dehnungen und Krümmungen für den ungerissenen und den vollständig gerissenen Querschnitt berechnet. Das gesamte Verfahren lässt sich in drei Schritten darstellen:

Berechnung der Schwindkräfte

Die durch Schwinden verursachten Kräfte werden anhand der nachstehenden Formeln auf der Grundlage der Schwinddehnung berechnet.

• N_shr = -ε_cs(t,ts)·Coef_ReinfΣ(E_si·A_si)
• M_shr,y = N_shr·e_shr,z
• M_shr,z = N_shr·e_shr,y

wobei

• e_shr,y = Σ(E_si·A_si)/ Σ(E_si·A_si·y_si) - t_iy
• e_shr,z = Σ(E_si·A_si)/ Σ(E_si·A_si·z_si) - t_iz
• E_si - Elastizitätsmodul des i-ten Bewehrungsstabs
• A_si - Fläche der Bewehrung des i-ten Bewehrungsstabs
• y_si - Position des i-ten Bewehrungsstabs vom Schwerpunkt des Querschnitts in y-Richtung
• z_{si -} Position des i-ten Bewehrungsstabs vom Schwerpunkt des Querschnitts in z-Richtung
• t_iy - Abstand zwischen dem Schwerpunkt des umgewandelten ungerissenen/gerissenen Querschnitts und dem Schwerpunkt des Betonquerschnitts in y-Richtung
• t_iz - Abstand zwischen dem Schwerpunkt des umgewandelten ungerissenen/gerissenen Querschnitts und dem Schwerpunkt des Betonquerschnitts in y-Richtung

Berechnung der durch Schwinden verursachten Dehnung und Krümmung

Strain and curvature caused by shrinkage are calculated for each element and these values are calculated for both states (uncracked and cracked cross-section). Calculation of strain caused by shrinkage:

• ε_sh = -ε_cs(t,ts)·Coef_Reinf·Σ(E_si·A_si)/(E_ceff·A_i)

Berechnung der Krümmung um die y- und z-Achse durch Schwinden 

• (1/r_y) = -ε_cs(t,ts)·Coef_Reinf·Σ(E_si·A_si·(t_iz-z_si))/(E_ceff·I_iy)
• (1/r_z) = -ε_cs(t,ts)·Coef_Reinf·Σ(E_si·A_si·(t_iy-y_si))/(E_ceff·I_iz)

Berechnung der Steifigkeiten für Schwinden

Die Steifigkeit des ungerissenen/gerissenen Querschnitts für das Schwinden wird aus der durch das Schwinden verursachten Dehnung und Krümmung unter Verwendung des Gesamtbelastungsniveaus (Gesamtlastkombination) berechnet und dann in der Finite-Elemente-Berechnung verwendet.

• Biegesteifigkeit um die y-Achse EI_y = M_tot,y/(1/r_y)

• Biegesteifigkeit um die z-Achse EI_z = M_tot,z/(1/r_z)

• Axialsteifigkeit  EA = N_tot/ε_sh

Hinweis: Wie oben angegeben, werden zur Vereinfachung die Gesamtkräfte anstelle der durch Schwinden verursachten Kräfte für die Berechnung der Steifigkeiten für die FEM-Analyse verwendet.

Ergebnispräsentation

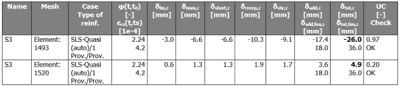
The output of the deflection results can be seen graphically in the 3D window and also numerically via the Brief, Standard or Detailed output. The following picture shows an example of the Brief table which represents the following values:

• Kriechfaktor  φ_(t,t0)
• Schwinddehnung  ε_(t,ts)
• Durchbiegung durch Kriechen  (δ_creep)
• Durchbiegung durch Schwinden (δ_shr)

Fallstudie

Die Auswirkungen des Schwindens werden anhand eines mittelgroßen Projekts veranschaulicht. Die Struktur hat eine Deckenstärke von 270 mm aus Beton C30/37, der durch eine ständige Last von 2,5 kN/m2 und eine veränderliche Last von 3,0 kN/m2 belastet wird. Die Bewehrung in beiden Flächen und Richtungen beträgt: Durchmesser 12/200 mm in der Spannweite und über den Stützen Durchmesser 12/100 mit B500B. Die Betondeckung beträgt 30 mm. Die Aushärtezeit des Betons beträgt 7 Tage, die Zeit der Lastaufbringung beträgt 28 Tage. Die Untersuchungszeit beträgt 50 Jahre. Die relative Luftfeuchtigkeit beträgt 50 %.

Es wird ein Vergleich zwischen den Ergebnissen der Durchbiegungen aus einer linearen und einer nichtlinearen Analyse angestellt, einschließlich Betonrissen und zeitabhängigen Effekten wie Kriechen und Schwinden.

• Nichtlineare Durchbiegung mit Rissbildung
  
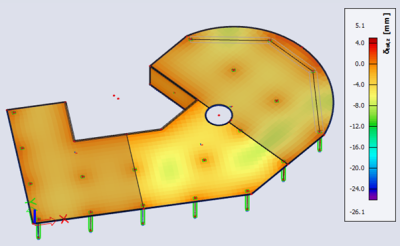
• Nichtlineare Verformung mit Rissbildung und Kriechen
  
• Nichtlineare Durchbiegung mit Rissbildung, Kriechen und Schwinden
  

Die vorherigen grafischen Ergebnisse lassen sich wie folgt zusammenfassen:

• Lineare Durchbiegung: maximale Verformung von 4,2 mm
• Nichtlineare Durchbiegung mit Rissbildung: maximale Verformung von 7,8 mm
• Nichtlineare Durchbiegung mit Rissbildung und Kriechen: maximale Verformung von 16,8 mm
• Nichtlineare Durchbiegung mit Rissbildung, Kriechen und Schwinden: maximale Verformung von 26,0 mm

Schlussfolgerungen

Wie aus den Ergebnissen ersichtlich ist, reicht eine rein lineare Analyse für Stahlbetonstrukturen nicht aus. Die Auswirkungen von Rissen führen zu fast doppelt so hohen Werten im Vergleich zur linearen Durchbiegung. Darüber hinaus ist es unerlässlich, auch Kriech- und Schwindverformungen zu berücksichtigen, um das tatsächliche Verhalten der Struktur zu ermitteln. Im Falle von Kriechen führt dies allein zu viermal höheren Ergebnissen und bei Berücksichtigung aller Effekte zusammen zu fast siebenmal höheren Ergebnissen. Werden solche Effekte bei der Planung vernachlässigt, kann dies zu erheblichen Problemen während der Lebensdauer der Struktur führen, insbesondere zu einer geringeren Gebrauchstauglichkeit aufgrund hoher Durchbiegungen.

Quellenangaben 

[1] EN1992-1-1 - Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings

[2] www.scia.net