Effets du retrait dans l'analyse non-linéaire

Lors de la conception de structures en béton, une analyse linéaire n'est généralement pas suffisante. Plusieurs autres aspects influencent le comportement de la structure, principalement aux états limites de service. Ces effets sont principalement les suivants :

• la fissuration du béton

• le fluage et le retrait

La fissuration du béton est généralement un effet irréversible qui apparaît lorsque la résistance à la traction du béton est dépassée. La structure peut toutefois être durable et fiable si les fissures sont inférieures aux limites imposées par la norme. Cet article traite principalement de la notification de ces effets lors de la conception, en mettant l'accent sur le retrait.

Effet de retrait

Les phénomènes de fluage et de retrait sont les caractéristiques qui dépendent du temps les plus importantes pour le béton. Lorsque le béton est mis en place, le ciment commence à s'hydrater en utilisant l'eau libre du mélange. Généralement, l'eau sort du béton et le processus de retrait de séchage commence. C'est la raison pour laquelle le béton doit être durci, en particulier dans les premières phases après le coulage. En l'absence d'un processus de cure spécial, des contraintes supplémentaires apparaissent à l'intérieur du béton, ce qui peut entraîner des fissures de retrait.
La deuxième partie du retrait est le retrait autogène lorsque le béton consomme sa propre eau pendant le processus de durcissement. Dans ce cas, l'ampleur du retrait autogène dépend principalement du rapport eau/ciment (w/c). Lorsque le rapport eau/ciment est plus faible, le retrait autogène est plus important.
Plusieurs paramètres influencent l'évolution du retrait :

• Le début et la durée du durcissement
• La quantité et la position des armatures
• La dimension de la structure
• L’humidité relative et la température
• Le type de ciment
• Etc

Rappels théoriques

Comme indiqué ci-dessus, la contrainte de retrait total (εcs(t,ts)) ) est composée de deux parties :

• le retrait de séchage (ε_cd(t,ts))
• le retrait autogène (ε_ca(t))

ε_cs(t,ts) = ε_cd(t,ts) + ε_ca(t)

Le calcul des deux contraintes est décrit directement dans la norme EN1992-1-1[1].

SCIA Engineer [2] prend en compte les deux parties des effets de retrait automatiquement par défaut (cette fonction peut être désactivée si nécessaire dans la Configuration Béton / Données de l'élément en béton). La valeur du retrait est calculée en fonction du temps de durcissement et du temps de chargement prédéfinis.

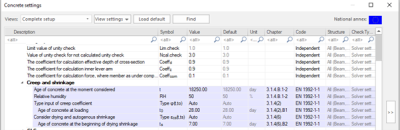
Les flèches dues au retrait sont calculées sur la base de la déformation et des courbures causées par les retraits pour la section non fissurée et entièrement fissurée. L'ensemble de la procédure peut être exprimé en trois étapes :

Calcul des efforts de retrait

Les efforts dus au retrait sont calculés selon les formules ci-dessous en fonction de la déformation de retrait.

• N_shr = -ε_cs(t,ts)·Coef_ReinfΣ(E_si·A_si)
• M_shr,y = N_shr·e_shr,z
• M_shr,z = N_shr·e_shr,y

où

• e_shr,y = Σ(E_si·A_si)/ Σ(E_si·A_si·y_si) - t_iy
• e_shr,z = Σ(E_si·A_si)/ Σ(E_si·A_si·z_si) - t_iz
• E_si  - est le module d'élasticité de la i-ième barre de ferraillage
• A_si - est la section de la i-ième barre de ferraillage
• y_si - position de la i-ième barre de ferraillage par rapport au centre de gravité de la section dans la direction y
• z_si - position de la i-ième barre de ferraillage par rapport au centre de gravité de la section dans la direction z
• t_iy - distance entre le centre de gravité de la section transformée non-fissurée/fissurée et le centre de gravité de la section en béton dans la direction y
• t_iz - distance entre le centre de gravité de la section transformée non-fissurée/fissurée et le centre de gravité de la section en béton dans la direction z

Calcul de la déformation et de la courbure causées par le retrait

La déformation et la courbure causées par le retrait sont calculées pour chaque élément et ces valeurs sont calculées pour les deux états (section non-fissurée et fissurée). La déformation causée par le retrait peut s’écrire comme suit:

• ε_sh = -ε_cs(t,ts)·Coef_Reinf·Σ(E_si·A_si)/(E_ceff·A_i)

Calcul de la courbure autour des axes y et z causée par le retrait 

• (1/r_y) = -ε_cs(t,ts)·Coef_Reinf·Σ(E_si·A_si·(t_iz-z_si))/(E_ceff·I_iy)
• (1/r_z) = -ε_cs(t,ts)·Coef_Reinf·Σ(E_si·A_si·(t_iy-y_si))/(E_ceff·I_iz)

Calcul des rigidités pour le retrait

La rigidité de la section non-fissurée/fissurée pour le retrait est calculée à partir de la déformation et des courbures causées par le retrait en utilisant le niveau total de charge (combinaison de charge totale) et est ensuite utilisée dans le calcul par éléments finis

• rigidité en flexion autour de l'axe y EI_y = M_tot,y/(1/r_y)
• rigidité en flexion autour de l'axe z EI_z = M_tot,z/(1/r_z)
• rigidité axiale EA = N_tot/ε_sh

Note : Comme indiqué ci-dessus, pour des raisons de simplification, les efforts totaux sont utilisés pour le calcul des raideurs pour l'analyse MEF au lieu des efforts causés par le retrait.

Présentation des résultats

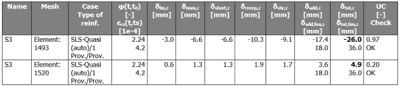
Les résultats de la flèche peuvent être visualisés graphiquement dans la fenêtre 3D et numériquement par le biais de la sortie brève, standard ou détaillée. L'image suivante montre un exemple du tableau bref qui représente les valeurs suivantes :

• coefficient de fluage φ_(t,t0)
• déformation de retrait ε_(t,ts)
• flèche due au fluage (δ_creep)
• flèche due au retrait (δ_shr)

Étude de cas

L'effet du retrait est illustré sur un projet de taille moyenne. La structure a une épaisseur de dalle de 270 mm en béton C30/37, qui est chargée par une charge permanente de 2,5 kN/m² et une charge variable de 3,0 kN/m². Le ferraillage sur les deux faces et dans les deux directions est du f12/200 mm dans la travée, et du f12/100 mm au-dessus des appuis, en B500B. L'enrobage du béton est de 30 mm. Le temps de durcissement du béton est de 7 jours, le temps d'application de la charge est de 28 jours. La durée de l'étude est de 50 ans. L'humidité ambiante relative est de 50 %.

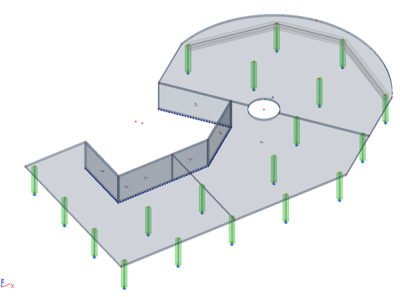
Une comparaison est faite entre les résultats des flèche provenant d'une analyse linéaire et ceux provenant d'une analyse non-linéaire, incluant la fissuration du béton et les effets fonction du temps comme le fluage et le retrait.

• Flèche non-linéaire avec fissuration
  
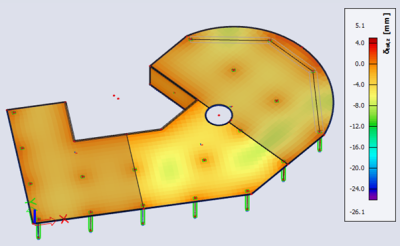
• Flèche non-linéaire avec fissuration et fluage
  
• Flèche non-linéaire avec fissuration, fluage et retrait
  

Les résultats graphiques précédents peuvent être résumés :

• Déformation linéaire : déformation maximale de 4,2 mm
• Déformation non-linéaire avec fissuration : déformation maximale de 7,8 mm
• Déformation non-linéaire avec fissuration et fluage : déformation maximale de 16,8 mm
• Déformation non-linéaire avec fissuration, fluage et retrait : déformation maximale de 26,0 mm.

Conclusions

Comme le montrent les résultats, l'utilisation d'une simple analyse linéaire n'est pas suffisante pour les structures en béton armé. L'effet de la fissuration donne des valeurs presque deux fois plus élevées que la flèche linéaire. De plus, il est essentiel de prendre en compte les effets du fluage et du retrait pour obtenir le comportement réel de la structure. Dans le cas du fluage uniquement, les résultats sont 4 fois plus élevés et lorsque tous les effets sont pris en compte, ils sont presque 7 fois plus élevés. Négliger ces effets lors de la conception pourrait entraîner des problèmes importants au cours du cycle de vie de la structure, en particulier une capacité de service réduite en raison de flèches élevées.

Références

[1] EN1992-1-1 - Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings
[2] www.scia.net