Stanovení součinitele kritického zatížení
Součinitel kritického zatížení se určí řešením úlohy vlastních čísel pomocí následující rovnice:
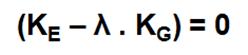
kde:
KE = elastická matice tuhosti EI
KG = geometrická matice tuhosti normálových sil T
Lambda = vlastní číslo = součinitel kritického zatížení
Elastická matice tuhosti je známá, protože představuje tuhost prvků konstrukce (sloupů, nosníků,...).
Geometrická matice tuhosti je korekční maticí pro získání reálnější tuhosti konstrukce. Účel geometrické matice tuhosti je vysvětlen na jednoduchém příkladu. Uvažujme nosník na dvou podporách, který je zatížen následujícím způsobem:
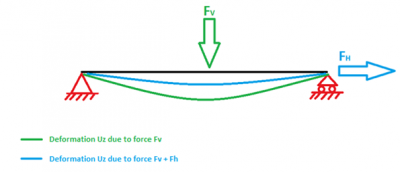
Pokud je nosník zatížen pouze svislým zatížením Fv, deformuje se podle zelené čáry. Hodnota deformace souvisí s elastickou tuhostí (matice tuhosti KE) daného prvku.
Tento nosník se bude deformovat méně (modrá čára), pokud bude kromě svislého zatížení Fv působit i vodorovné zatížení FH. Toto vodorovné zatížení FH má ztužující účinek na svislou deformaci nosníku. Tento ztužující účinek je zohledněn v geometrické matici tuhosti KG. Matice KG je vlastně korekcí matice KE, aby bylo možné získat realistické výsledky konstrukce. SCIA Engineer hledá při výpočtu stability hodnotu lambda, která splňuje následující rovnici:
KE = Lambda x KG.
To se provádí řešením matic tuhosti výše uvedené rovnice. Níže najdete příklad takových matic tuhosti (KE a KG).
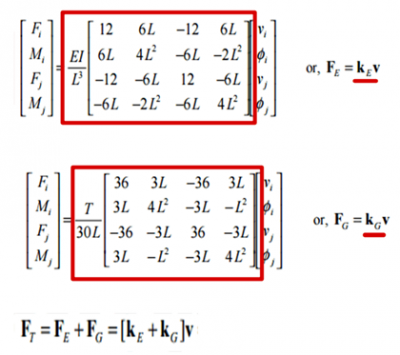
Další informace:
Po určení součinitele kritického zatížení pomocí stabilitního výpočtu může uživatel určit kritickou normálovou sílu Ncr, která způsobuje nestabilitu (=vybočení) konstrukce. Protože Ncr = alfakritické x NEd (vzorec 5.1 normy EN1993-1-1; Lambda = alfakritické).
Když je známé Ncr, tak je možné určit součinitele vzpěru ky a kz, protože součinitele vzpěru jsou jedinými neznámými v Eulerově vzorci:
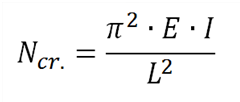
kde:
- L = vzpěrná délka = ky x systémová délka yy nebo kz x systémová délka zz