Determination critical load coefficient

The critical load coefficient is determined by solving an eigenvalue problem via the following equation:

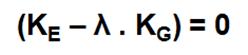
With:

• K_E = Elastic stiffness matrix EI
• K_G = Geometrical stiffness matrix of the normal forces T
• Lambda = eigenvalue = critical load coefficient

The elastic stiffness matrix is known because it represents the stiffness of the structure elements (columns, beams,…).
The geometrical stiffness matrix is a correction matrix to get a more realistic stiffness of the structure. I will explain the purpose of the geometrical stiffness matrix with a simple example. Consider a beam on two supports which is loaded as follows:

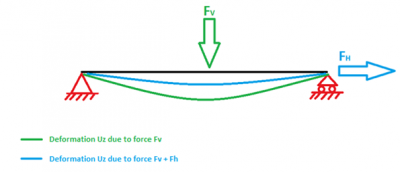
The beam will deform according to the green line if it is only loaded by the vertical load F_V. The value of the deformation is related to the elastic stiffness (Stiffness matrix K_E) of that element.
This beam will deform less (blue line) when there is besides the vertical load F_V a horizontal load F_H. This horizontal load F_H has a stiffening effect on the vertical deformation of the beam. This stiffening effect is taken into account in the geometrical stiffness matrix K_G. K_G is in fact a correction on K_E in order to get realistic results of the structure. SCIA Engineer searches during the stability calculation for a lambda value that fulfills the following equation
K_E = Lambda x K_G.
This is done by solving the stiffness matrices of the above equation. Below you can find an example of such stiffness matrices (K_E & K_G).

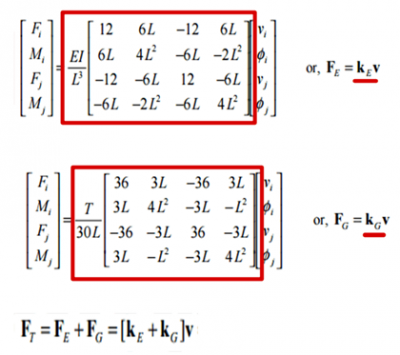
Extra information:
Once the critical load coefficient is determined via the stability calculation the user can determine the critical normal force N_Cr. that causes instability (=buckling) of the structure. Because N_Cr. = alpha_critical x N_ed (Formula 5.1 of EN1993-1-1; Lambda = alpha_critical).

The user can also determine the buckling factors k_y & k_z when he knows N_Cr. Because the buckling factors are the only unknowns in the formula of Euler:

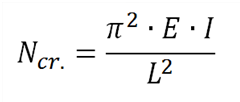
With:

• L=bucklinglength = k_y x systemlength yy or k_z x systemlenght zz