Kritische belastingcoëfficiënt bepalen
De kritische belastingcoëfficiënt wordt bepaald door het eigenwaarde probleem op te lossen via de volgende vergelijking:
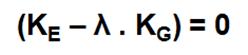
met:
- KE = elastische stijfheidmatrix EI
- KG = geometrische stijfheidmatrix van de normaalkrachten T
- Lambda = eigenwaarde = kritische belastingcoëfficiënt
De elastische stijfheidmatrix is gekend want dit is de stijfheid van uw structuurelementen (kolommen, balken,...). De geometrische stijfheidsmatrix is een soort van correctiematrix om de stijfheid van uw structuur beter te benaderen. Ik illustreer de functie van deze geometrische stijfheidsmatrix aan de hand van een simpel voorbeeld, beschouw een balk op twee steunpunten:
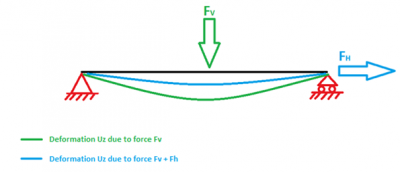
De balk zal vervormen volgens de groene lijn als deze enkel verticaal belast wordt door FV. De waarde van de verticale vervorming is gerelateerd aan de elastische stijfheid (Elastische stijfheidmatrix KE) van dit element.
Deze balk zal minder doorbuigen (blauwe lijn) als er naast de verticale kracht FV ook een trekkracht FH op zit. Je kunt dus zeggen dat deze trekkracht een verstijvende werking heeft op de doorbuiging van de balk. Deze verstijvende werking wordt in rekening gebracht via de geometrische stijfheidmatrix KG. KG voert dus in feite een correctie uit op uw elastische stijfheidmatrix KE om de realiteit beter te benaderen. Tijdens een stabiliteitsberekening wordt er dusdanig gezocht naar een lambda (=kritische belastingcoëfficiënt) die ervoor zorgt dat KE = Lambda x KG
Dit wordt gedaan door de stijfheidmatrices van bovenstaande vergelijking op te lossen. Hieronder een voorbeeld van zo een stijfheidmatrix (KE en KG)
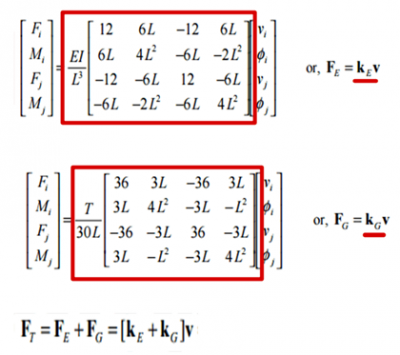
Extra informatie:
Eens de kritische belastingcoëfficiënt bepaald is kan men tevens NCr (kritische normaalkracht dat knik veroorzaakt) bepalen want NCr. = alphacrit. x Ned (Formule 5.1 van EN1993-1-1; Lambda = alpha_critical)
Nadat de NCr. gekend is kun je simpelweg aan de hand van de formule van Euler de ky of kz knikfactoren bepalen vermits deze de enige onbekenden zijn in de vergelijking.
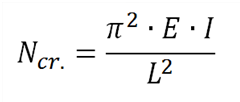
(met L = kniklengte = ky x systeemlengte yy of kz x systeemlengte yy)