Détermination du coefficient de la charge critique.
Le coefficient de la charge critique est déterminé par la résolution d’un problème de mode propre à partir de l’équation suivante :
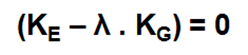
Ke =Matrice de rigidité élastique EI
Kg = Matrice de rigidité géométrique des forces normales T
Lambda = Valeur propre = Coefficient de charge critique
La matrice de rigidité élastique est connue puisqu’elle représente la raideur des éléments de structure (poutres, poteaux …).
La matrice de rigidité géométrique est une matrice de correction pour obtenir une rigidité plus réaliste de la structure. Le but de la matrice de rigidité est expliqué avec un simple exemple. Considérons une poutre sur deux appuis: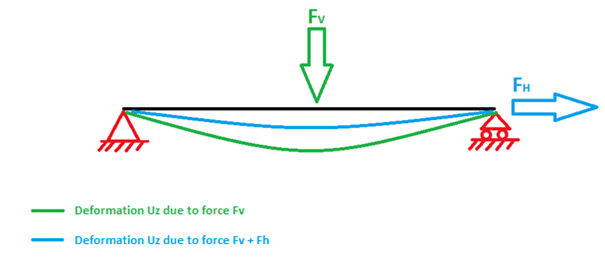
La poutre va se déformer selon la ligne verte si elle est seulement chargée par la charge verticale Fv. La valeur de la déformation est liée à la raideur élastique (matrice de rigidité Ke) de cet élément.
La déformation va être réduite (ligne bleue) quand la poutre est chargée par une force horizontale Fh en plus de la charge vertical Fv. Cette force horizontale Fh augmente la rigidité de la poutre vis-à-vis la déformation verticale. L’effet sur la rigidité est pris en compte par la matrice de rigidité géométrique Kg qui est en effet une correction sur Ke afin d’obtenir des résultats plus proches de la réalité. Lors d’un calcul de stabilité, SCIA Engineer cherche une valeur Lambda qui satisfait l’équation suivante:
Ke = Lambda x Kg.
Ci-dessous un exemple des matrices de rigidité Ke et Kg.
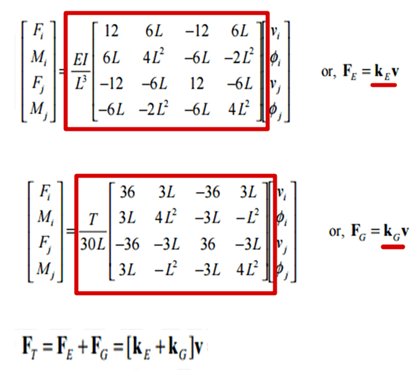
Informations supplémentaires:
Une fois le coefficient de charge critique est déterminé par le calcul de stabilité, l’utilisateur peut déterminer la force normale critique Ncr qui provoque l’instabilité (=flambement) de la structure.
Ncr = alpha_critique x Ned (Formule 5.1 du EN1993-1-1; Lambda = alpha_critique).
L’utilisateur peut également déterminer les coefficients de flambement Ky et Kz après avoir déterminer Ncr en utilisant la formule d’Euler :
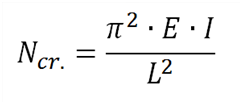
(Avec L=Longueur de flambement = Ky x longueur du système yy ; kz x longueur du système zz)