Warum hat die Rippe eine Normalkraft?
In SCIA Engineer wird die Rippe als ein exzentrischer Balken in die Platte integriert. Die Exzentrizität wird als ½ Plattendicke und ½ Balkenhöhe ermittelt:
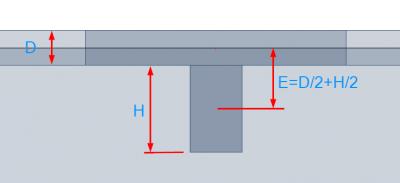
Beim Erstellen des Trägerquerschnitts definiert man als Querschnittshöhe die Höhe „H“ zwischen der Unterkante der Rippe und der Unterkante der Platte (wenn es sich um ein Unterzug handelt).
Durch die Verschiebung der Neutralachse ändern sich die Schnittgrößen im Gesamtsystem und aus einem einfachen Biegemoment beim System ohne Exzentrizität entstehen im Model auch Normalkräfte.
Bei einem Unterzug erhalten wir in der Regel Druckkraft in der Platte und Zugkraft im Unterzug.
Der exzentrische Balken verursacht Normalkräfte in der Platte:
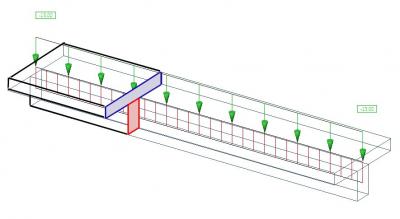

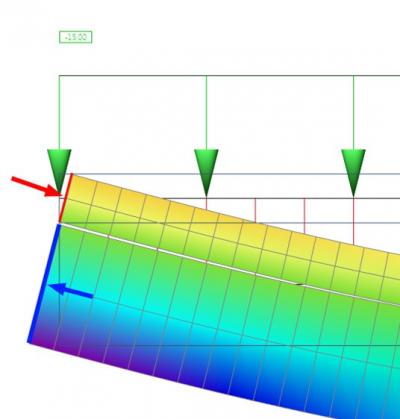
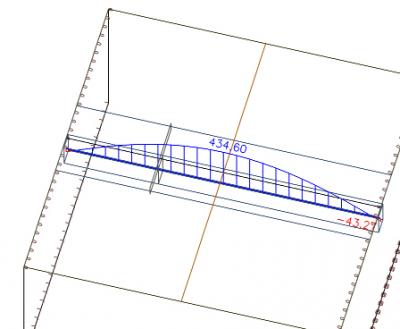
Diese resultieren aus der Verformung des Plattenbalken Systems. Im Bild die „ux“ einmal in 3D nur um das Model zu erläutern. Dieses Model wurde aus 2 rechteckquerschnitten mit starren Kupplungen erstellt. Die horizontale Verformung ist erlaubt, damit kein Zwang entsteht.
Hier die horizontale Verformung in der Seitenansicht:
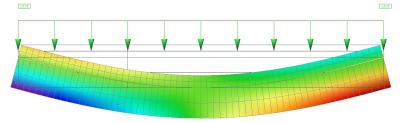
Betrachtet man den Anfang des Balkens, so sieht man Druck in der Platte (roter Pfeil) und Zug im Balken (blauer Pfeil).
Natürlich muss das gesamte System im Gleichgewicht sein und die gesamte Axialkraft (als Summe der Axialkraft in der Platte und der Axialkraft im Balken) muss Null sein.
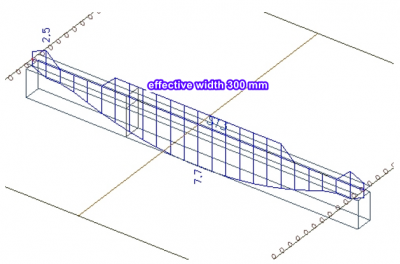
In unserem Model haben wir nur ein Balken und wir haben auch alle Schnittgrößen des oberen Teils in der Normalkraft. In der Praxis, ist aber die Mittwirkende Plattenbreite aber kleiner als die Gesamtbreite der Platte. Nur in Ausnahmefällen sind die Rippen so angeordnet, dass wir mit der mittwirkenden Plattenbreite alle Schnittgrößen sammeln können. Das wäre der Fall, wenn die Rippen dicht nebeneinander liegen und der Abstand der Rippen gleich oder kleiner wäre, als die Mittwirkende Plattenbreite in der Norm.
Das Verhalten der Rippe in einer breiten Platte
Wir können nun ein System untersuchen, bei dem die Breite der Platte größer ist als die effektive Breite der Rippe. Die Gleichgewichtsbedingung muss erfüllt sein. Wenn wir alle Axialkräfte in der gesamten Platte und im Balken integrieren, erhalten wir - natürlich - ein Null-Ergebnis.
Wir betrachten die Verteilung der Axialkraft in der Platte. Diese ist unabhängig von der definierten effektiven Breite der Platte. Nur die Steifigkeiten der Platte und des Trägers sind für die Form der Verteilung der Schnittgrößen verantwortlich.
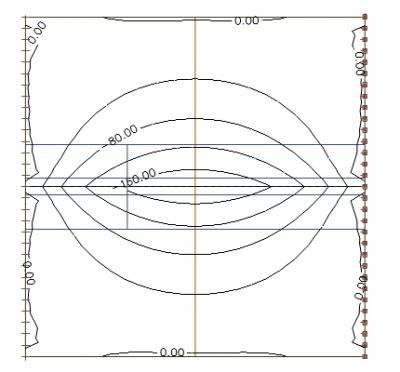
Wir sehen uns einen Schnitt durch die Mitte der Platte an, der die Verteilung der Axialkraft zeigt:
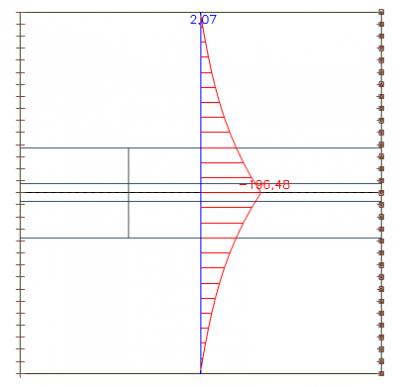
Wir können die Axialkraft im Querschnitt über die gesamte Breite der Platte integrieren. Wir erhalten einen Wert von 439 kN.
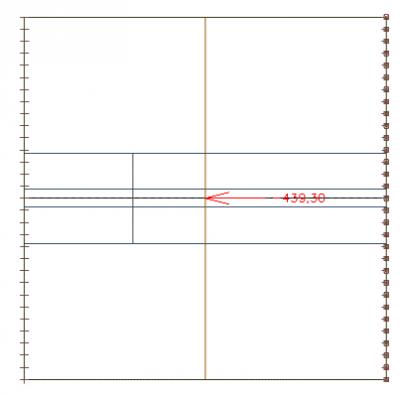
Wir können diesen Wert mit der Axialkraft im Balken vergleichen, die 435 kN beträgt. Wir sehen, dass sich das gesamte System im Gleichgewicht befindet. Der geringe Unterschied ergibt sich aus der Größe der finiten Elemente.
Das Verhalten einer Rippe für unterschiedliche mittwirkende Plattenbreiten
Wenn wir jedoch die wirksame Breite der Rippe auf die gesamte Breite der Platte ausdehnen, vernachlässigen wir die Verteilung der Schnittgrößen über die Platte und die Konzentration über den Balken (tatsächlich gibt es zwei Grenzwerte: die minimale wirksame Breite ist gleich der Breite des Balkens und die maximale gleich der gesamten Breite der Platte).
Die inneren Kräfte in der Platte werden von der Platte ausgeschlossen und in einen neuen virtuellen T-Querschnitt integriert. Dieser virtuelle Querschnitt besteht aus der effektiven Plattenbreite und dem Träger.
Wir betrachten die Verteilung der Axialkraft in der Platte. Wir sehen, dass diese Verteilung derjenigen in einem früheren Bild entspricht, in dem die effektive Breite der Rippe gemäß dem Code definiert wurde.
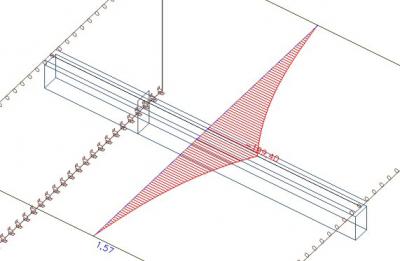
In der Abbildung ist die Axialkraft zu sehen, nachdem die Kräfte innerhalb der wirksamen Breite der Rippe aus der Platte herausgerechnet wurden. In SCIA Engineer können Sie dies über das Kontrollkästchen "Rippe" in den Ergebnissen erreichen.
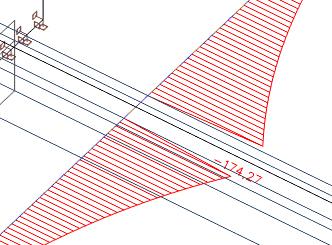
Diese Axialkräfte innerhalb der effektiven Breite der Platte können integriert werden.
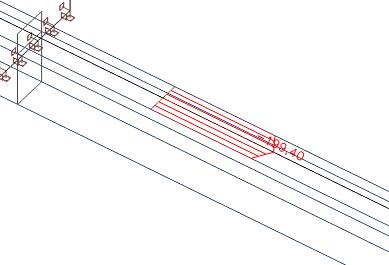
Wir erhalten eine Axialkraft von 57 kN, die sich in der Platte befindet. Die gesamte Axialkraft in der Platte beträgt 435 kN. Daher haben wir in dem Teil außerhalb der wirksamen Breite als Axialkraft 435 kN - 57 kN = 378 kN.
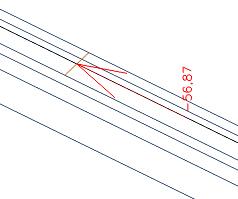
Im Balken haben wir immer noch dieselben 445 kN (der Unterschied zu den vorherigen Bildern ergibt sich aus der veränderten Größe der 2D-Finite-Elemente).
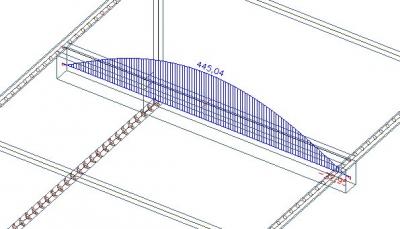
Wenn wir die Summe der integrierten Axialkraft in der Platte und im Träger bilden, müssen wir 445 kN - 57 kN = 388 kN erhalten.
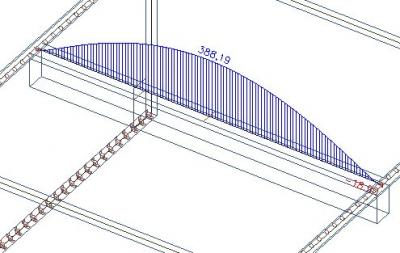
Sehen Sie sich an, was passiert, wenn wir die effektive Breite der Rippe auf 1500 mm erhöhen. Dies ergibt sich aus der folgenden Formel: 2 * (0,1 * L) + bw = 2 * 0,6 + 0,3
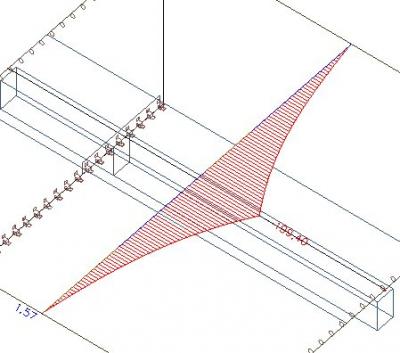
Wie wir sehen können, ist die Axialkraft in der Platte immer noch die gleiche. Das muss so sein, denn die effektive Breite der Rippe hat keinen Einfluss auf die Verteilung der Axialkraft in der Finite-Elemente-Berechnung. Sie beeinflusst nur die Aufteilung der Kräfte nach der Berechnung zwischen der Platte und dem virtuellen T-Profil.
Der Bereich der wirksamen Breite der Rippe wird aus der Platte entfernt und die Kräfte werden in den T-Querschnitt integriert. Die inneren Kräfte außerhalb der Platte verbleiben in der Platte.
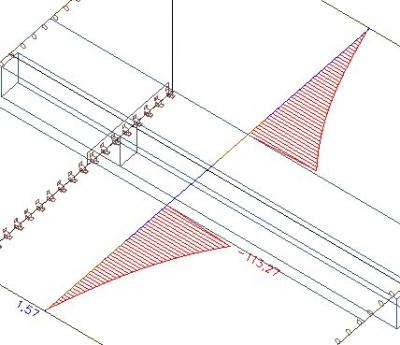
Diese inneren Kräfte werden in den Abschnitt T verlagert.

Integriert man die Axialkräfte, erhält man 234 kN.
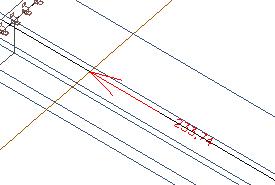
Im rechteckigen Abschnitt unter der Platte erhalten wir die ursprünglichen 445 kN.
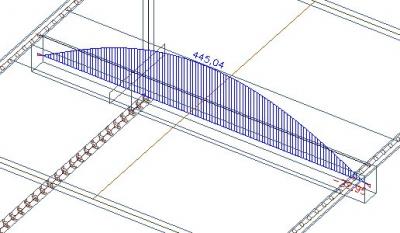
Reduziert man diese Axialkraft des Trägers um 234 kN, also die Summe der Axialkräfte aus der wirksamen Breite der Rippe, erhält man 211 kN.

Die Axialkraft außerhalb der wirksamen Breite verbleibt in der Platte.
Integriert man die Kräfte (links und rechts) außerhalb der wirksamen Breite, erhält man eine Axialkraft von 210 kN, die mit der Spannung in der Rippe als T-Profil im Gleichgewicht steht.
Zusammengefasst
Im System muss Gleichgewicht herrschen. In unserem vereinfachten System, wo wir keine horizontale Kräfte haben und auch keine horizontale Reaktionen produzieren müssen wir insgesamt in dem Platten+Balken System eine Normalkrat = 0 haben.
Die Normalkraft wird auf die Platte und den Unterzug verteilt. Diese müssen sich ausgleichen.
Die Mittwirkende Plattenbreite dient zur nachträglichen Umschichtung der Kräfte (N, Vz, My, Mx) zwischen der Platte und einem virtuellen T Querschnitt. Sie hat keinen Einfluss auf die Schnittgrößen des FE Modells.
Die Gesamtdruckkraft der Platte ist gleich wie die Zugkraft im Rechteckträger unter der Platte. Wenn wir in den virtuellen T Querschnitt aber nur ein Teil dieser Druckkraft verschieben, bleibt in der Platte eine nicht berücksichtigte Druckkraft (keine Angst, dass wir die vergessen, die wird in der Bemessung der Plattenbewehrung sehr wohl berücksichtigt). Und genau diese nicht berücksichtigte Druckkraft der Platte ist gleich der Zugkraft des T Querschnitts.
Es gibt auch andere Möglichkeiten eine Rippe zu definieren.
Man kann ein T Querschnitt ohne Exzentrizität eingeben. Damit beeinflusst man aber die Verteilung der Steifigkeiten zwischen der Platte und dem Träger. Die Interpretation der Mittwirkenden Plattenbreite hat hier einen direkten Einfluss auf die Schnittgrößen der Platte und des Trägers. Vorteil dieses Systems ist, dass man kleine Normalkräfte erhält, weil keine Exzentrizität im System vorhanden ist. Ein Nachteil ist das Gewicht. Der T Querschnitt hat sein Eigengewicht und der summiert sich mit dem Gewicht der Platte. Dann hat man das Gewicht der Platte 1x im System. Auch ein Nachteil ist, dass sich die Bewehrung der Platte und die Bewehrung des Trägers überlappen und man muss es manuell in der Dokumentation der Berechnung aufteilen.
Weiter kann man ein Ersatzrechteck definieren. Prinzip ist, dass das Platten+Balken System (T Querschntit) ein Trägheitsmoment hat. Dieses wird durch ein Teil der Platte und ein Teil des Rechteckquerschnitts ersetzt. Das Rechteck der Platte und das Rechteck des Trägers müssen das gleiche Trägheitsmoment haben wie das ursprüngliche T Querschnitt. Nachteil ist, die Bemessung. Die müsste man in einem anderen Modell machen und die Schnittgrüßen manuell übertragen. (Erklärung findet man in Günter Rombach: Anwendung der Finite-Elemente-Methode im Betonbau)
Vergleichen wir nun die untere Bewehrung in dem Plattenbalken, für unterschiedliche mittwirkenten Plattenbreiten.
Wir sehen, dass für 300mm (Breite des Trägers), 1500mm (Normwert) und 2500mm (willkürlich definiert nur wegen dem Vergleich) die untere Bewehrung immer gleich ist. Auf die Bewehrung hat auch die Querkraft einen Einfluss, aus der auch eine Zugkraft entsteht.