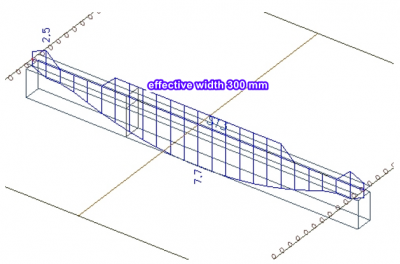
Normaalkracht in een rib

Ribben zijn een belangrijk onderdeel van constructies. Vroeger berekenden ingenieurs hun constructies als 2D platen, terwijl ribben werden benaderd als een meewerkende T sectie. Bij 3D schaalmodellen kunnen ribben echter precieser gemodelleerd worden als excentrische staven. Bijgaand artikel gaat in op de evaluatie van interne krachten in deze ribben.

SCIA Engineer integreert de ribben als excentrische balken bevestigd aan platen. De excentriciteit E wordt berekend uit de helft van de plaatdikte D en de helft van de hoogte van de doorsnede van de balk H.

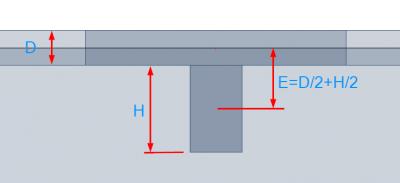
Bij het invoeren van de doorsnede van de balk, wordt de hoogte van de doorsnede gedefinieerd als de afstand tussen de onderzijde van de plaat en de onderzijde van de balk. In bovenstaande afbeelding wordt deze hoogte gemarkeerd als “H”.

Door de verschuiving van de neutrale as veranderen de interne krachten in het hele systeem. In een eenvoudig systeem, dat slechts onderworpen is aan een buigend moment, krijgen we een structuur met zowel een inwendig buigend moment als een axiale kracht. Gewoonlijk, als de balk zich onder de plaat bevindt, krijgen we druk in de plaat en trek in de balk.

De excentrische balk veroorzaakt axiale krachten in de plaat. Dit blijkt uit de vervorming van het gehele plaat + balk systeem. Onderstaande afbeelding toont de horizontale vervorming “ux” om grafisch het gedrag van het systeem te verklaren. Dit systeem bestaat uit twee balken met een rechthoekige doorsnede, die verbonden zijn met starre bindingen. De horizontale verplaatsing van de ondersteuning is vrij.

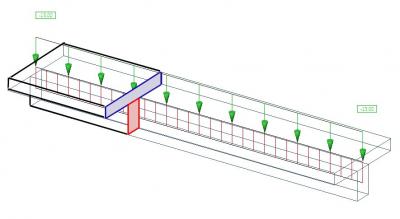
De horizontale vervorming in zijaanzicht:

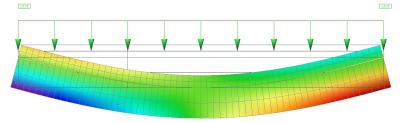
Als je het begin van de balk uitvergroot, zie je druk in de plaat (rode pijl) en trek in de balk (blauwe pijl).

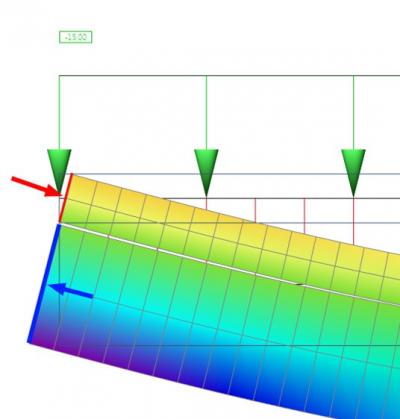
Het hele systeem moet in evenwicht zijn an de totale normaalkracht (de som van de normaalkracht in de plaat en de balk) moet gelijk zijn aan nul.

­

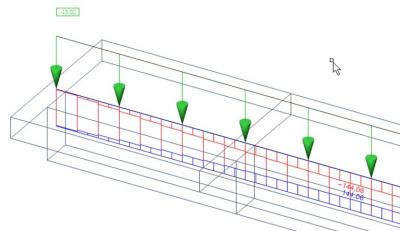
In ons model hebben we enkel een balk beschouwd, waardoor alle interne krachten van het bovenste deel zijn geïntegreerd in de axiale kracht in de rib. Praktisch gezien is de effectieve breedte van de rib kleiner dan de volledige breedte van de plaat. Slechts bij uitzondering zijn de ribben zodanig geplaatst dat er geen ruimte is tussen de effectieve breedtes, waardoor alle interne krachten in de plaat kunnen worden opgeteld in de rib. Dit komt voor als de afstand tussen de ribben kleiner is of gelijk aan de effectieve breedte van de rib berekend uit de nationale norm.

Gedrag van een rib in een grote plaat

Nu kunnen we een systeem onderzoeken waarbij de breedte van de plaat groter is dan de effectieve breedte van de rib. De evenwichtsvoorwaarde moet worden voldaan. Als we al de axiale krachten integreren in de volledige plaat en de balk, krijgen we – uiteraard – een resultaat gelijk aan nul.

We kijken naar de verdeling van de normaalkracht in de plaat. Deze is onafhankelijk van de bepaalde effectieve breedte van de plaat. Enkel de stijfheid van de plaat en de balk zijn verantwoorfelijk voor de vorm van de verdeling van interne krachten.

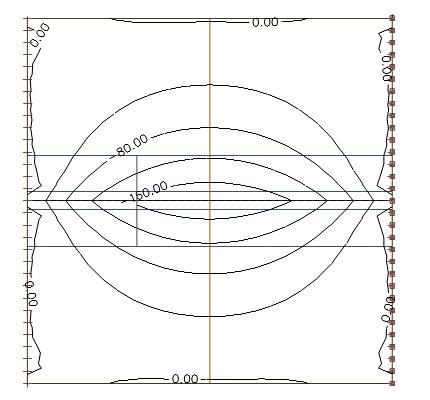
We bekijken een sectie doorheen het midden van de plaat die de verdeling van de normaalkracht weergeeft:

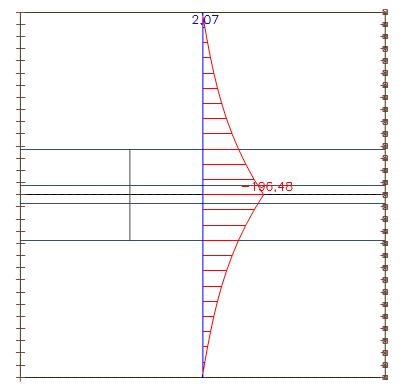
Als we de normaalkracht integreren volgens dezelfde sectie over de volledige breedte van de plaat, bekomen we een waarde van 439kN

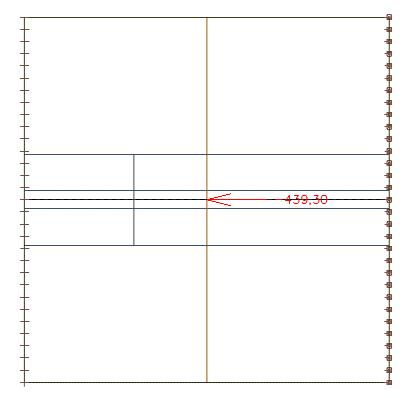
Vergeleken met de axiale kracht van 435 kN in de balk, zien we dat het hele systeem in evenwicht is. Het kleine verschil ontstaat door de grootte van de eindige elementen.

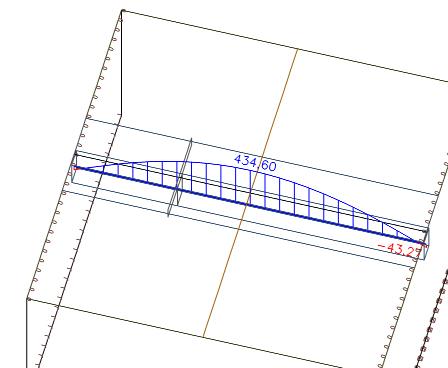
Vergelijking van verschillende effectieve breedtes

Als we echter de effectieve breedte van de rib vergroten tot de volledige breedte van de plaat, verwaarlozen we de verdeling van de interne krachten over de plaat en de concentratie in de balk (in feite zijn er twee grenswaarden: de minimale effectieve breedte is gelijk aan de breedte van de balk en de maximale is gelijk aan de volledige breedte van de plaat).

De interne krachten in de plaat worden uitgesloten van de plaat en geïntegreerd in een nieuwe virtuele T doorsnede. Deze virtuele doorsnede bestaat uit het plaatdeel met de breedte gelijk aan de effectieve breedte van de rib en uit de balk.

We bekijken de verdeling van de axiale kracht in de plaat. We zien dat de verdeling gelijk is aan die in de eerdere afbeelding, waar de effectieve breedte van de rib werd gedefinieerd volgens de norm.

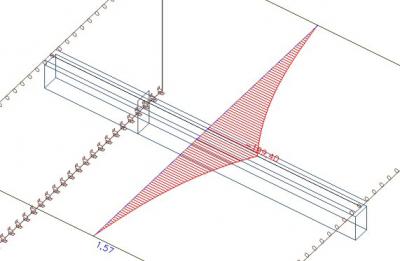
Op de volgende afbeelding zien we de axiale kracht, nadat de krachten binnen de effectieve breedte van de rib werden uitgesloten van de plaat. In SCIA Engineer kan je dit laten weergeven met behulp van de checkbox “RIB” in het resultaten menu.

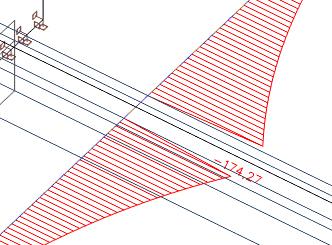
We kunnen de axiale krachten in de effectieve breedte van de rib integreren.

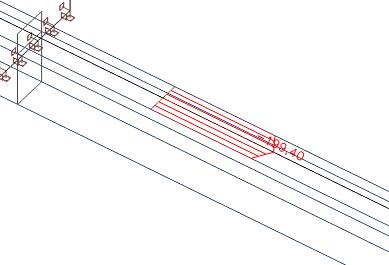
We krijgen dan een axiale kracht van 57 kN in de plaat. De totale axiale kracht in de plaat was 435 kN. Daarom hebben we in het deel buiten de effectieve breedte een axiale kracht van 435 kN - 57 kN = 378 kN.

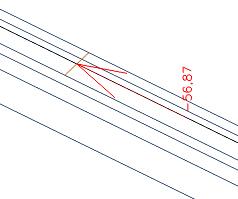
In de balk hebben we nog steeds dezelfde waarde van 445 kN (het verschil met de vorige afbeeldingen ontstaat door de aangepaste grootte van de 2D eindige elementen).

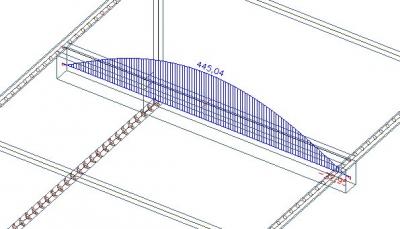
Als we de som maken van de geïntegreerde axiale kracht in de plaat en in de balk, krijgen we 445 kN - 57 kN = 388 kN.

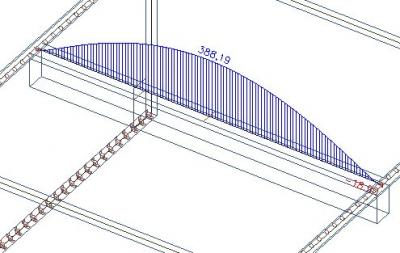
Kijk wat er gebeurt als we de effectieve breedte van de rib verhogen tot 1500 mm. Dit volgt uit de volgende formule: 2 * (0,1 * L) + b_w = 2 * 0,6 + 0,3.

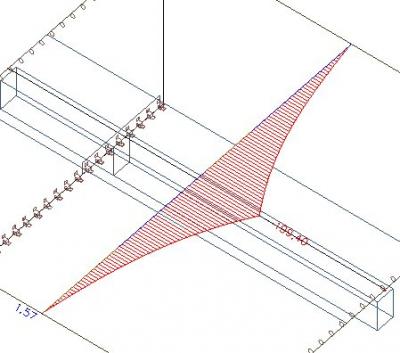
Zoals we kunnen zien, is de axiale kracht in de plaat nog steeds hetzelfde. Dit klopt aangezien de effectieve breedte van rib geen invloed heeft op de verdeling van de axiale kracht in de eindige elementen berekening. Het heeft alleen invloed op de splitsing van de krachten na de berekening tussen de plaat en de virtuele T doorsnede.

Het gebied van de effectieve breedte van de rib wordt uit de plaat verwijderd en we integreren de krachten in de T doorsnede. De interne krachten buiten de rib zullen in de plaat blijven.

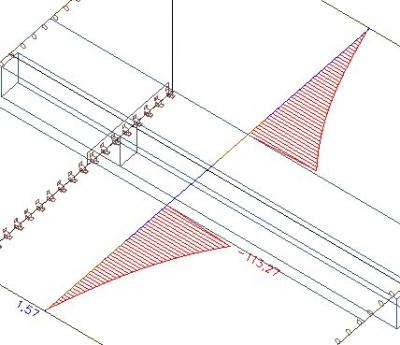
Deze interne krachten worden verplaatst naar de T doorsnede.

Als we de axiale krachten integreren, krijgen we 234 kN.

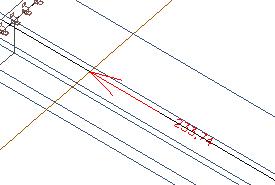
In de rechthoekige doorsnede onder de plaat krijgen we de oorspronkelijke waarde van 445 kN.

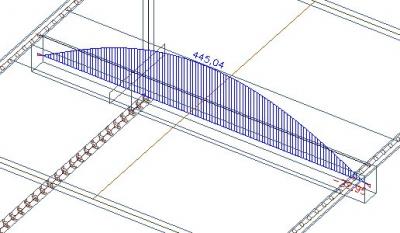
Als we deze axiale kracht van de balk verminderen met 234 kN (dat de som is van de axiale krachten van de effectieve breedte van de rib), bekomen we 211 kN.

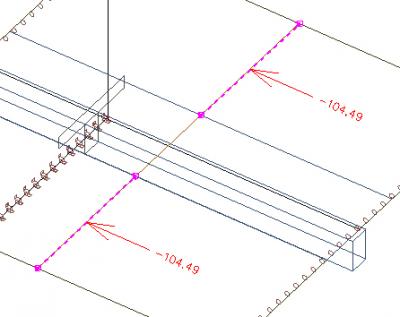
De axiale kracht buiten de effectieve breedte blijft in de plaat.

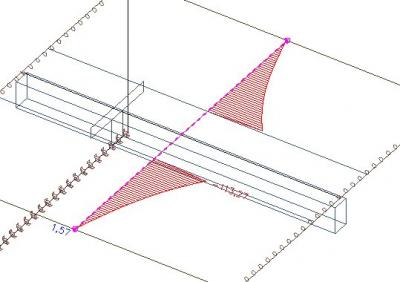
Als we de krachten (links en rechts) buiten de effectieve breedte integreren, krijgen we een axiale kracht gelijk aan 210 kN, die in evenwicht is met de trek in de rib (beschouwd als een T doorsnede).

 

Conclusie

Het systeem moet in evenwicht zijn. In het vereenvoudigde systeem bestaande uit een plaat en balk zonder horizontale krachten, moeten we nul axiale krachten hebben als integratie.

De interne krachten (in onze tekst onderzochten we alleen axiale kracht) zullen worden verdeeld tussen de plaat en rib. Deze moeten in evenwicht zijn.

De effectieve breedte van de rib zal alleen worden gebruikt voor herberekening van de interne krachten (N, Vz, My, Mx) tussen de plaat en de virtuele T-balk. Het heeft geen invloed op de interne krachten in het eindige elementen model.

De som van de axiale krachten in de gehele plaat moet gelijk zijn aan de axiale kracht in de rechthoekige balk onder de plaat. Als we slechts een deel van deze axiale krachten binnen de effectieve breedte verplaatsen, blijven sommige delen van de axiale krachten als druk in de plaat buiten de effectieve breedte (geen angst, deze krachten worden behandeld bij het ontwerp van wapening in de plaat). En de niet-beschouwde axiale kracht blijft als trek in de virtuele T doorsnede van de rib.

Er zijn ook andere mogelijkheden om een rib te modelleren.
Je kan een T doorsnede definiëren zonder excentriciteit. Op die manier beïnvloed je de verdeling van de stijfheden tussen de plaat en de balk. De definitie van de effectieve breedte van de rib heeft een directe invloed op de stijfheid van het systeem en op de interne krachten. Het voordeel is dat je geen axiale kracht in de T doorsnede krijgt want er is geen excentriciteit. Anderzijds krijg je een iets hoger eigengewicht, omdat het gewicht van de T doorsnede en de plaat wordt verdubbeld. Een ander nadeel is dat je wapening in de balk en in de plaat krijgt en je dit moet vermelden in de documentatie.

 

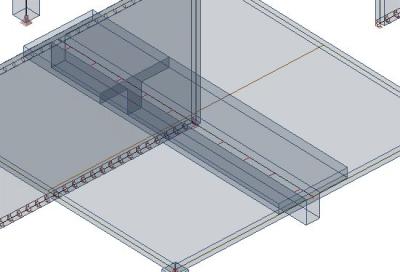
Een andere optie is om een vervangende rechthoekige doorsnede te definiëren. Het principe is dat het traagheidsmoment van het plaat+balk systeem hetzelfde moet zijn als deze van een T doorsnede met een rechthoekige balk en effectieve breedte van de rib. Hieruit kan je de hoogte van de vervangende rechthoekige doorsnede afleiden (je kan hierover meer informatie vinden in “Günter Rombach: Anwendung der Finite-Elemente-Methode im Betonbau").

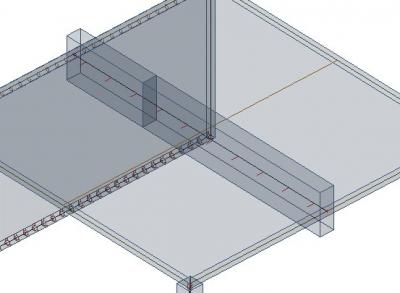
Tot slot vergelijken we de onderwapening in de rib voor verschillende effectieve breedtes.

We vergelijken drie varianten: een effectieve breedte van 300 mm (de breedte van de balk), een effectieve breedte van 1500 mm (volgens EN 1992) en een willekeurige effectieve breedte van 2500 mm.

Ook een dwarskracht beïnvloedt het resultaat van de langswapening, omdat een deel van de dwarskracht naar de beugels gaat, een deel naar de betondrukschoor en een deel naar de langswapening.