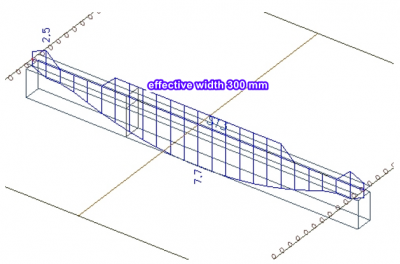
Force axiale dans les nervures

Les nervures font partie intégrante des structures. Dans le passé, les ingénieurs calculaient les structures comme des dalles 2D et les nervures étaient incluses approximativement (comme une section en T). Avec les modèles de coque 3D, les nervures peuvent être modélisées plus précisément comme des poutres excentriques. Cet article explique l'évaluation des forces internes des nervures.

SCIA Engineer intègre les nervures comme des poutres excentrées liées à la dalle. Cette excentricité E est calculée à partir de la moitié de l’épaisseur de la dalle D et la moitié de la hauteur de la section de la poutre H.

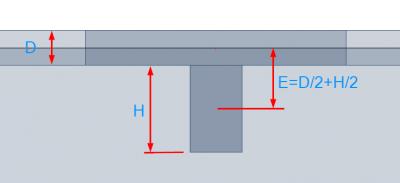
Lorsque vous créez une poutre, sa hauteur est définie comme la distance entre la face inférieure de la dalle et le bas de la poutre. Elle est notée “H” sur l’image.

A cause du saut de l’axe neutre, les efforts internes dans le système changent. Dans un système simple soumis à un moment de flexion seul, nous obtenons une structure avec des efforts normaux en plus du moment.

Généralement, lorsque la poutre se situe en-dessous de la dalle, il y a de la compression dans la dalle et de la traction dans la poutre.

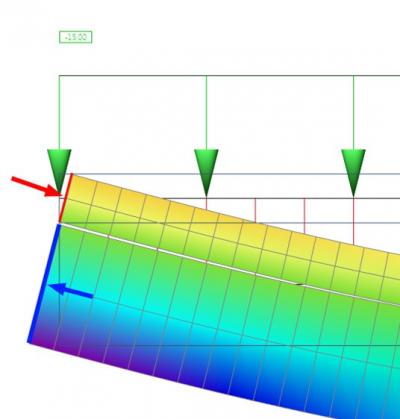
La poutre excentrée induit des efforts normaux dans la dalle qui résultent de la déformation de l’ensemble dalle + poutre. L’image ci-dessous représente la déformation horizontale “ux”. Elle explique graphiquement le comportement de la structure. Pour cet exemple, nous avons utilisé deux poutres de sections rectangulaires connectés par des bras rigides. Le déplacement horizontal de l’appui est libre.

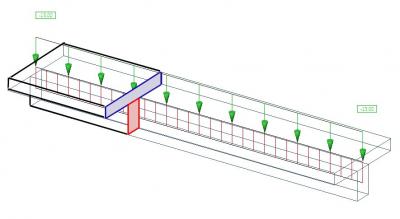
Déformation horizontale avec vue en long.

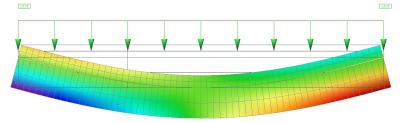
Si l'on regarde le début de la poutre, on peut voir une compression dans la dalle (flèche rouge) et une traction dans la poutre (flèche bleue).

Bien entendu, l'ensemble du système doit être en équilibre et la force axiale totale (soit la somme de la force axiale dans la dalle et de la force axiale dans la poutre) doit être nulle.

 

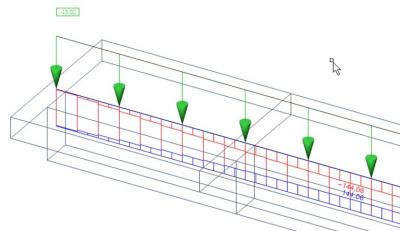
Dans l’exemple, nous n’avons qu’une seule poutre et la totalité des efforts dans la partie supérieure est intégrée dans l’effort normal dans la nervure. Dans la pratique, la largeur efficace de la dalle est plus petite que sa largeur totale. Ce n'est qu'exceptionnellement que les nervures sont disposées de manière à ce qu'il n'y ait pas d'écart entre les largeurs efficaces, de sorte que tous les efforts internes de la dalle puissent être repris par la nervure. C’est le cas par exemple lorsque la distance entre nervures est plus petite ou égale à la largeur efficace dans la dalle calculée selon la norme.

Comportement d'une nervure dans une dalle

Nous allons dans la suite, regarder un exemple avec une largeur efficace plus petite que la largeur de la dalle. La condition d’équilibre doit être vérifiée et la résultante d’effort normal dans la dalle et la poutre doit être nulle.

Nous examinons la distribution de l'effort axial dans la dalle. Celui-ci est indépendant de la largeur efficace définie de la dalle. Seules les rigidités de la dalle et de la poutre sont responsables de la forme de la distribution des efforts internes.

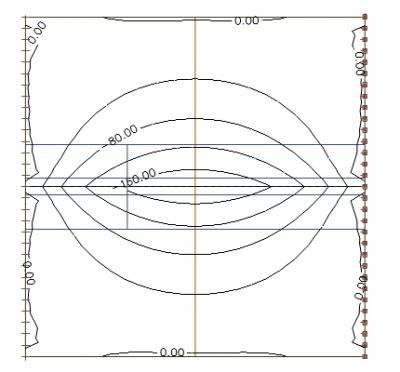
Nous regardons une section au milieu de la dalle montrant la distribution de l'effort axial :

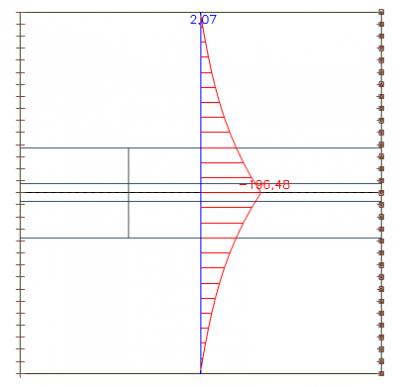
Nous pouvons intégrer l'effort axiale dans la section sur toute la largeur de la dalle. Nous obtenons une valeur de 439 kN.

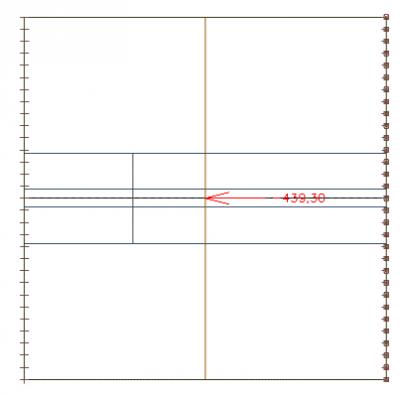
Nous pouvons comparer cette valeur avec l'effort axial dans la poutre, qui est de 435 kN. Le système est donc bien en équilibre. La petite différence entre les deux résultats d’effort normal provient de la taille du maillage.

 

 

 

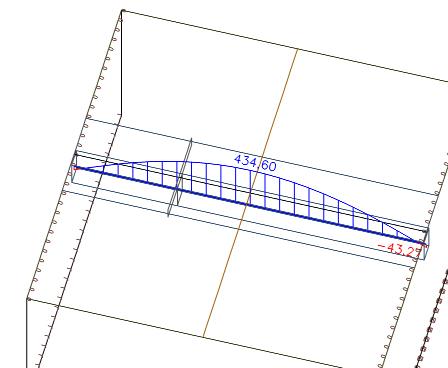
Comparaison de différentes largeurs efficaces

Si la largeur efficace est égale à toute la largeur de la dalle, la répartition de l'effort dans la dalle est négligée au profit d'une concentration d'effort dans la poutre. (Il y a deux valeurs limites: la largeur efficace minimale correspond à la largeur de la poutre et la largeur efficace maximale à celle de la dalle.)

Les efforts internes de la dalle sont exclus de la dalle et intégrés dans une nouvelle section fictive en T. Cette section fictive est composée de la poutre et de la largeur efficace dans la dalle.

Nous considérons la distribution de l'effort axial dans la dalle. Nous pouvons voir que cette distribution est égale à celle d'une image précédente où la largeur effective de la nervure était définie selon la norme.

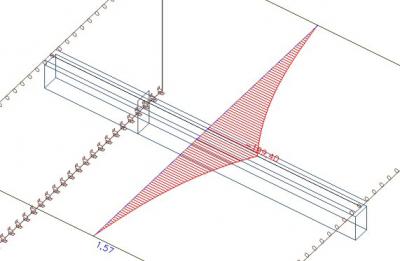
Sur l'image, nous pouvons voir l'effort axial après que les efforts compris dans la largeur efficace de la nervure ont été exclus de la dalle. Dans SCIA Engineer, vous pouvez réaliser cette opération en cochant la case "nervure" dans les résultats.

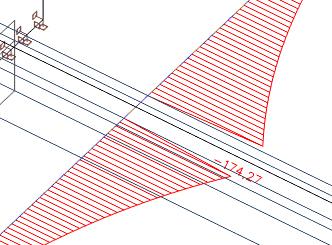
Ces efforts axiaux dans la largeur efficace de la dalle peuvent être intégrés.

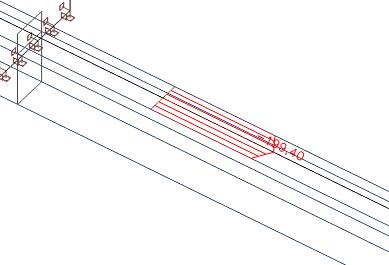
On obtient un effort axial égale à 57 kN, qui se trouve dans la dalle. L'effort axial total dans la dalle est de 435 kN. Par conséquent, dans la partie située à l'extérieur de la largeur efficace, nous avons comme force axiale 435 kN - 57 kN = 378 kN.

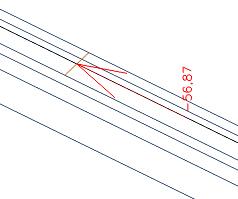
Dans la poutre, il y a toujours les 445kN (La différence par rapport au cas précédent provient de la modification de la taille du maillage des éléments 2D).

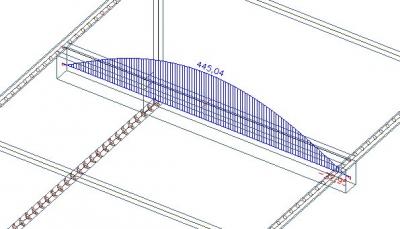
La somme des efforts normaux dans la poutre et dans la largeur efficace est de 445-57=388kN.

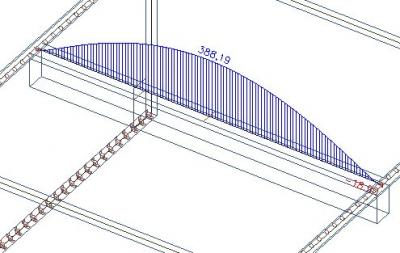
Nous allons augmenter la largeur efficace à 1500mm. Cette largeur est calculée suivant la formule: 2 * (0,1 * L) + b_w = 2*0,6+0,3.

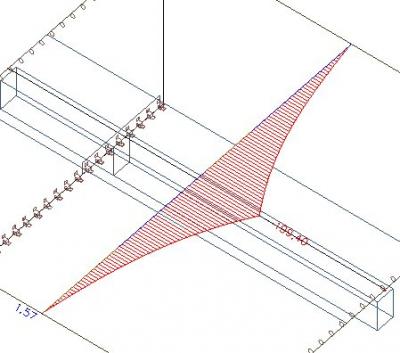
L’effort normal dans la dalle reste le même car la largeur efficace n’a pas d’influence sur la répartition d’effort normal dans le calcul par éléments finis. La largeur efficace influence uniquement la répartition d’effort entre la dalle et la section virtuelle en T après le calcul.

Les efforts au niveau de la largeur efficace sont retirés de la dalle et intégrés dans la section en T. En dehors de la largeur efficace, les efforts restent dans la dalle.

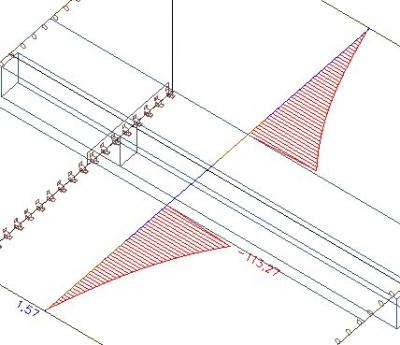
Les efforts dans la largeur efficace seront transférés à la section en T.

La résultante d’effort normal est de 234kN.

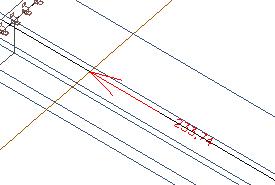
Dans la section rectangulaire au-dessous de la dalle nous retrouvons les 445kN initiaux.

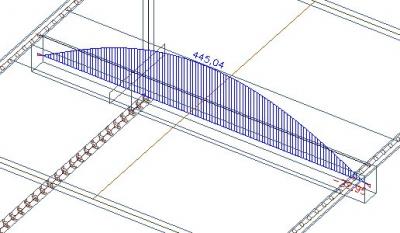
Si nous déduisons l'effort axial de la barre de 234 kN, ce qui représente la somme des efforts normaux dans la largeur efficace, nous obtenons 445-234=211kN.

Les efforts normaux en dehors de la largeur efficace reste dans la dalle.

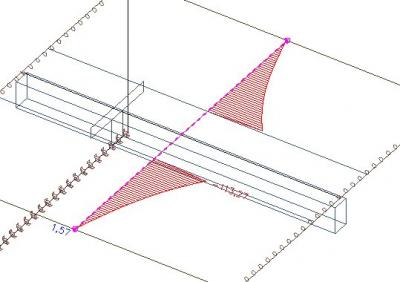
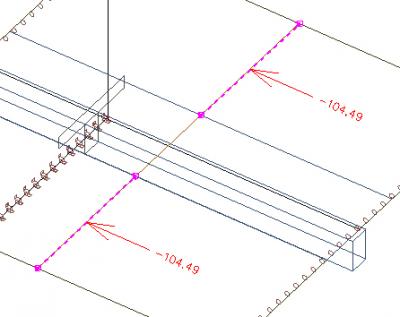
Les efforts résultants (à droite et à gauche) de la largeur efficace donne 210kN. Cet effort est en équilibre avec la traction dans la nervure en T.

 

Conclusion

L’ensemble doit être en équilibre.  Pour notre exemple simplifié, composé d’une dalle et d’une poutre sans efforts horizontaux, la résultante d’efforts normaux doit être nulle.

Les efforts, dans l’exemple nous n’avons étudié que l’effort normal, seront redistribués entre la dalle et la nervure. Ces derniers doivent être en équilibre.

La largeur efficace  est utilisée uniquement pour la redistribution des efforts internes (N, Vz, My, Mx) entre la dalle et la poutre virtuelle en T. Elle n’influence pas le calcul des efforts internes dans le modèle éléments finis.

L’effort normal total dans la dalle doit être égale à celui dans la poutre rectangulaire située en-dessous. Si nous ne déplaçons qu'une partie de ces efforts axiaux à l'intérieur de la largeur efficace, certaines parties des efforts axiaux restent en compression dans la dalle à l'extérieur de la largeur efficace (ne vous inquiétez pas : ces forces seront traitées lors de la conception du ferraillage dans la dalle). Et l'effort axial non pris en compte reste sous forme de tension dans la section virtuelle en T de la nervure.

Il y a également d'autres options pour modéliser une nervure.

Vous pouvez définir une section en T sans excentricité. Avec ce type de modélisation, vous influencez la répartition de la rigidité entre la dalle et la poutre. La largeur efficace de la dalle aura une influence directe sur la rigidité du système et donc sur la répartition des efforts. L’avantage est qu’il n’y a pas d’efforts normaux dans la section en T car il n’y a pas d’excentricité. L’inconvénient est que le poids propre est légèrement plus important car le poids de la section en T et de la dalle, au niveau de la largeur efficace, sont pris en compte deux fois. Aussi, il y aura un ferraillage dans la poutre et une dans la dalle qu'il faudra mentionner dans votre rapport.

 

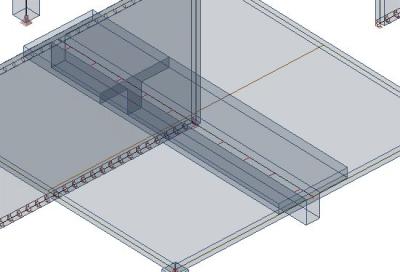
Une autre option consiste à définir une section rectangulaire équivalente. Le principe est que le moment d’inertie du système dalle + poutre doit être le même que la section en T avec la poutre rectangulaire et largeur efficace de la nervure. Vous en déduirez alors la hauteur de la section rectangulaire équivalente. (Vous trouverez plus de détails dans “Günter Rombach: Anwendung der Finite-Elemente-Methode im Betonbau).

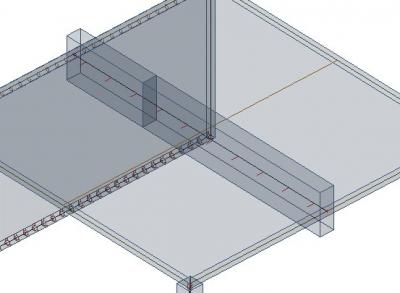
Comparons maintenant les armatures supérieures dans la nervure pour différentes largeurs efficaces.

Nous comparerons 3 variantes:

• une largeur efficace de 300mm (largeur de la poutre
• une largeur de 1500mm provenant de l’EN 1992
• une largeur arbitraire de 2500mm

L'efffort de cisaillement influence également le calcul du ferraillage longitudinale, car une partie de l'effort de cisaillement va aux étriers, une partie à la bielle de compression en béton et une partie au ferraillage longitudinale.