Analýza druhého řádu

Výpočty podle teorie druhého řádu zohledňují postupné deformování konstrukce vlivem aplikovaného zatížení. Řečeno matematicky, působící zatížení je rozděleno na malé části (přírůstky) a pro každý přírůstek se vypočítá a změní tuhost konstrukce. 

Účinky 2. řádu se také někdy nazývají účinky P-Δ a p-δ a ve SCIA Engineer (a také jinde) se na ně odkazuje jako na geometrickou nelinearitu. 

Podívejme se na některé opakující se dotazy našich uživatelů.  

 

Kdy musím provádět výpočty podle teorie druhého řádu?

Jednotlivé části Eurokódů (EC2, EC3, EC4, EC atd.) určují v kapitole 5 (Analýza konstrukce), kdy je nutno výpočet podle teorie druhého řádu provádět. U ocelových konstrukcí například nízká hodnota součinitele α_cr naznačuje vysokou ohebnost (štíhlost) konstrukce a tudíž citlivost na počáteční imperfekce a příčné deformace. 

Součinitel α_cr se určí jako podíl pružného kritického vzpěrného zatížení pro mód globální nestability F_cr a návrhového zatížení konstrukce F_Ed. Jinými slovy, abychom určili, zda je nutno provádět výpočet podle teorie druhého řádu, musíme se spolehnout na výsledky stabilitního výpočtu. 

Ve SCIA Engineer můžeme vytvořit stabilitní kombinace z vybraných návrhových kombinací a získáme kritické součinitele vzpěru, jež odpovídají těmto zatěžovacím scénářům. Tyto součinitele jsou vlastně násobiteli zatížení, které je obsaženo ve stabilitní kombinaci. A protože naše stabilitní kombinace jsou „návrhové zatížení“, jsou tyto součinitele právě našimi součiniteli α_cr , které hledáme. 

Je také důležité si uvědomit, jaký typ konečně-prvkového výpočtu chceme provádět, abychom získali návrhové vnitřní síly. Chceme zůstat u pružného výpočtu, nebo chceme také použít plastické klouby a redistribuovat momenty? Podle EC3 platí, že pokud provádíme pružný výpočet a kterýkoli z našich součinitelů α_cr je menší než 10, pak musíme konstrukci navrhovat na výsledky výpočtu podle teorie druhého řádu. V případě plastického výpočtu (např. plastických kloubů) je pak limitní hodnotou pro nutnost provádět výpočet podle teorie druhého řádu α_cr < 15.

 

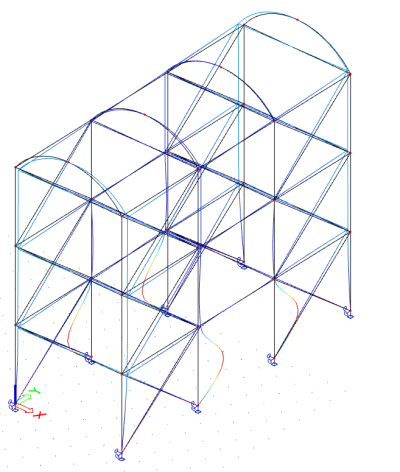
Jak mohu zohlednit celkové deformace podle normy?

Geometrické imperfekce v konečně-prvkovém modelu zaručují, že účinky druhého řádu jsou při výpočtu správně zohledněny. Ti z Vás, kteří dobře znají kapitolu 5 v EC3, se často ptají, jak ve SCIA Engineer zohlednit celkové imperfekce a imperfekce dílce. 

Imperfekce se definují na úrovni nelineární kombinace: každá nelineární kombinace může mít svoji sadu imperfekcí. To je výhodné, protože různé zatěžovací scénáře vedou k jinému módu selhání, který je naopak větší či menší měrou ovlivněn tvarem konkrétní imperfekce. 

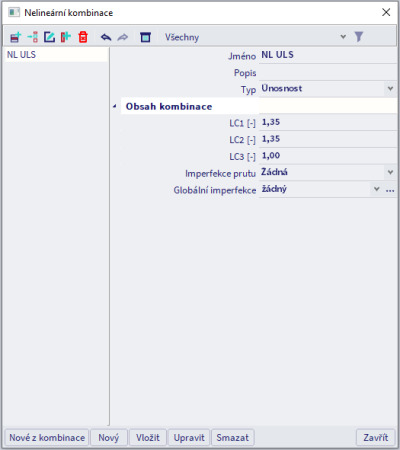
Globální nedokonalosti jsou definovány a uloženy ve zvláštní knihovně, kterou lze otevřít přímo v dialogu nelineárních kombinací nebo prostřednictvím Knihovny > Případy zatížení, Kombinace > Globální nedokonalosti. 

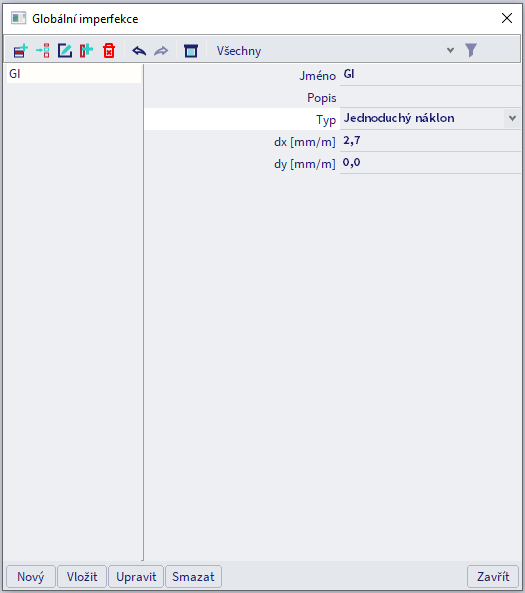
Pro definování rovnoměrného horizontálního posunu konstrukce použijte zadání typu „Jednoduchý náklon“ a zadejte relativní náklon ve směru osy X a Y - dx a dy. Kapitola 5.3.2 v EC3 obsahuje obrázek 5.2 s úhlem náklonu φ. V dialogu pro zadání nelineární kombinace použijte dx = 1000*φx (nebo dx = 1000*tan(φx), podle toho, jakým způsobem obrázek interpretujete). Typ imperfekce „jednoduchý náklon“ se hodí pro konstrukce s pravidelným půdorysem i bokorysem.

 

Existují pro celkové imperfekce různé způsoby zadání?

Ano, ve SCIA Engineer existuje několik možností. Jmenovitě jsou to:

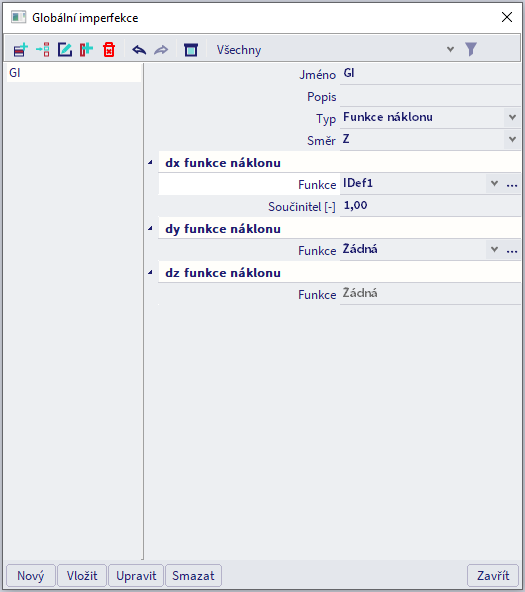
• Funkce náklonu: pokud potřebujete po výšce budovy měnit velikost nebo i směr náklonu, použijete pro definování funkci náklonu. Tyto funkce se zadávají ručně jako lomené křivky složené z několika (mnoha) přímých úseků a zadávají se ve funkci Knihovny > Konstrukce, Výpočet > Počáteční imperfekce.  

• Imperfekce odvozené ze zatěžovacího stavu: SCIA Engineer umožňuje spočítat deformaci konstrukce pro daný zatěžovací stav a spočtenou deformaci aplikovat jako počáteční imperfekci. Pokud víte, jaký přibližný tvar imperfekcí chcete získat, můžete definovat zatěžovací stav, který takovou deformaci způsobí. Můžete zadat zatěžovací stav se zlomkem všech návrhových zatížení, tak si můžete být jisti, že ve výpočtu budou zastoupeny všechny možné stabilitní účinky.  

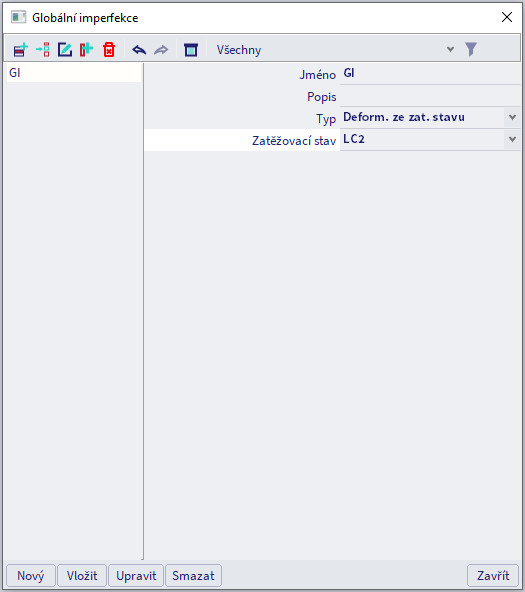
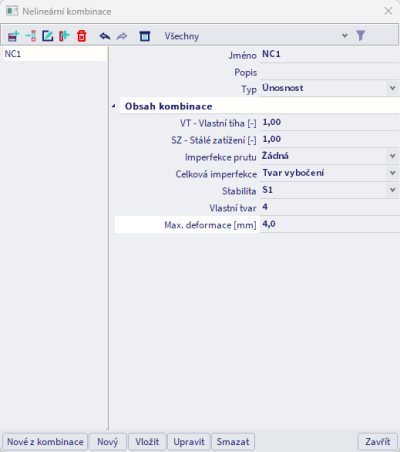
• Vlastní stabilitní tvar jako imperfekce: můžete zvolit stabilitní kombinaci a jeden z jejích vlastních tvarů a ten aplikovat jako imperfekci konstrukce. 

 

Jak mohu zohlednit lokální deformace podle normy?

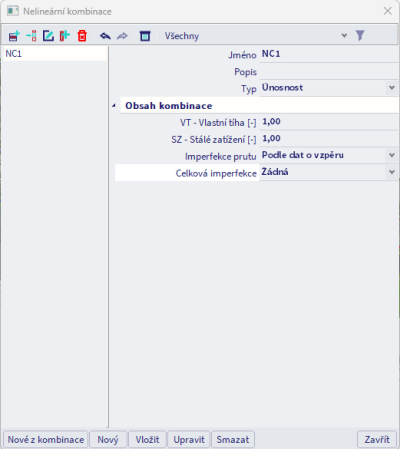
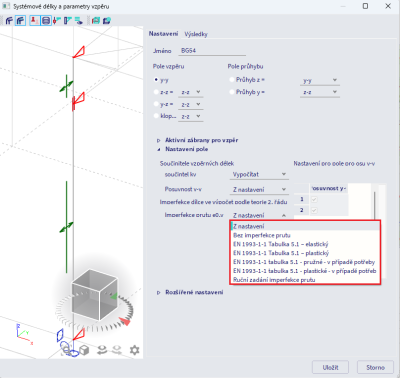
Jak bylo uvedeno již dříve, imperfekce se přiřazují nelineární kombinaci. Nejpraktičtějším způsobem přiřazení hodnoty imperfekce je odkázat se na nastavení vzpěru (přes nastavení kombinace). Tím lze přes nastavení vzpěru určit, který z dílců vykazuje imperfekce. Je často dobré uvažovat imperfekce na dílcích, které chcete analyzovat podrobně, raději, než přiřadit imperfekce všem dílcům na konstrukci. 

 

Existují pro lokální imperfekce různé způsoby zadání?

Ano. Namísto odkazu na data o vzpěru umožňuje SCIA Engineer definovat lokální imperfekce přímo pomocí vlastností nelineární kombinace. Pamatujte však, že zadaná křivost bude pak aplikována na všechny dílce v konstrukci.  

 

Co znamená funkcionalita "Geometrická nelinearita"?

Geometrická nelinearita se týká výpočtu druhého řádu. Pokud je tato funkcionalita zapnutá a provedeme analýzu druhého řádu, bude se zatížení aplikovat po jednotlivých přírůstcích a podle toho se bude konstrukce postupně deformovat. To vše v závislosti na nastavení řešiče. Proto se výsledky budou lišit od lineární analýzy, bez ohledu na to, zda jsou použity počáteční imperfekce nebo ne. Pro správné zachycení důležitých nelineárních efektů je však vhodné imperfekce zohlednit.

Poznámka: Geometrická nelinearita se bere v úvahu v nelineární analýze, která se provádí pro nelineární kombinace. Účinky druhého řádu nejsou ve výsledcích lineární analýzy přítomny. Lineárně řešené zatěžovací stavy jsou superponovány, aby se získaly výsledky lineárních kombinací. V nelineárním kontextu princip superpozice neplatí, protože účinky zatížení ovlivňují účinky jiných zatížení.

Jak vypočítat amplitudu imperfekce při použití tvaru vybočení?

Rámy:

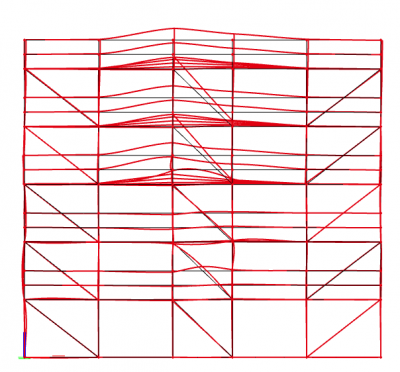
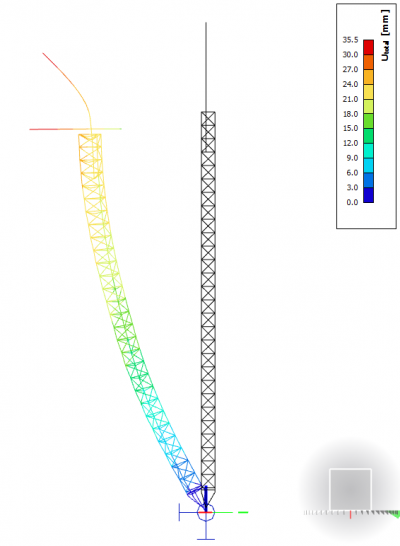
EN 1993-1-1 poskytuje v §5.3.2 (11) návod, jak vypočítat amplitudu jedné společné globální i lokální imperfekce za použití tvaru vybočení odvozeného přímo z analýzy stability (η_init). Tato metoda je platná pro rámy a vyžaduje, aby byla amplituda odvozena ručně a poté vložena do SCIA Engineer. Volba tvaru imperfekce je také na vás.

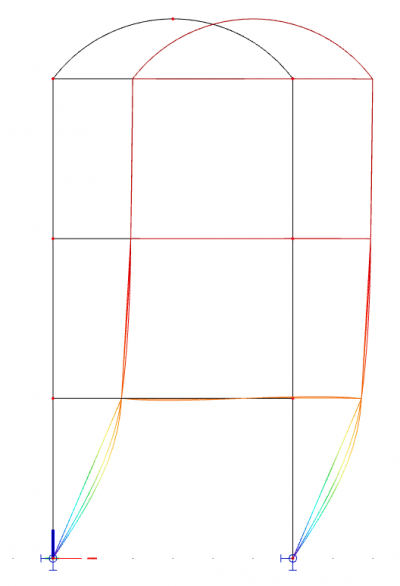
Tato metoda zohlednění imperfekcí vyžaduje definování kombinací zatížení pro samotnou analýzu stability a poté vizuální zkontrolu získaných tvarů vybočení. Měl by být použitý nejnižší tvar kritického vybočení, který představuje celkovou deformaci konstrukce ve zkoumaném směru. Tvar imperfekce a její amplituda jsou opět zadány pro nelineární kombinaci.
Pro stanovení amplitudy imperfekce je třeba získat několik vstupů z FE modelu, z výsledků lineární a stabilitní analýzy a také z Posudku oceli.

Imperfekce se stanoví takto:

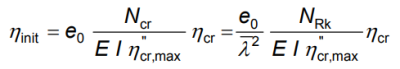
Kde:

• η_cr: tvar kritického vybočení konstrukce v pružném stavu

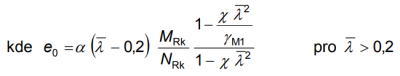
poměrná štíhlost konstrukce:

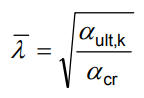
• χ: součinitel vzpěrnosti pro příslušnou křivku vzpěrné pevnosti, určenou pro příslušný průřez, viz 6.3.1
• α: imperfekce pro příslušnou křivku vzpěrné pevnosti, viz tabulky 6.1 a 6.2
• α_ult,k: nejmenší násobitel soustavy osových sil N_Ed v prutech pro dosažení charakteristické únosnosti N_Rk v nejvíce osově namáhaném průřezu bez uvážení vzpěru
• α_cr: tvar kritického vybočení konstrukce v pružném stavu
• M_Rk: charakteristická únosnost rozhodujícího průřezu v ohybu, například M_el,Rk nebo M_pl,Rk
• N_Rk: charakteristická únosnost rozhodujícího průřezu při působení osové síly N_pl,Rk
• EIη"_cr,max: ohybový moment vyvolaný imperfekcí η_cr v rozhodujícím průřezu

Z výše uvedeného je patrné, že musíme určit:

• kritický průřez v konstrukci (kde účinky zatížení vedou k maximálnímu poměru využití v lineárním kontextu)
• nejvíc tlačený dílec v konstrukci.

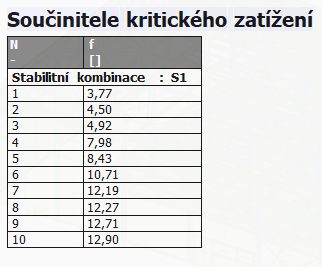
α_ult,k, M_Rk, N_Rk, χ a α lze získat z posudku oceli. α_cr a (EIη"_cr,max) lze získat z výsledků stabilitní analýzy.

 

Desky:

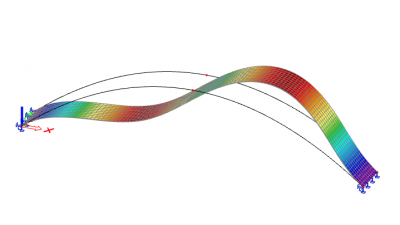
Pro konstrukce modelované pomocí 2D deskových prvků platí podobný postup, ale amplituda imperfekcí by měla být určena z EN 1993-1-5 Přílohy C. Opět platí, že pro správné zohlednění všech potenciálních způsobů selhání vzpěru je třeba provést nelineární analýzu druhého řádu s počátečními imperfekcemi.

Díky všestrannosti 2D modelů lze teoreticky zachytit všechny režimy selhání. Je ale třeba vhodně nastavit:

• síť konečných prvků
• formulaci prvků pro ohyb a smyk
• a zahrnutí imperfekcí

To se liší od rámových konstrukcí, kde jsou vyžadována dodatečná ověření klopení.

EN 1993-1-5 Příloha C nabízí v podstatě dvě možnosti pro zohlednění imperfekcí:

a) Explicitní modelování geometrických a materiálových imperfekcí:

• geometrické imperfekce mohou vycházet z kritických tvarů boulení stěn, přičemž amplitudy jsou brány jako 80 % výrobních tolerancí
• materiálové imperfekce (např. reziduální napětí) mohou být reprezentovány obrazcem napětí odpovídajícím výrobě s amplitudami rovnými očekávaným (středním) hodnotám

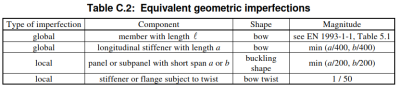
b) Modelování tvaru a amplitudy imperfekce podle zjednodušeného přístupu uvedeného v tabulce C.2. V tomto případě jsou geometrické i meteriálové imperfekce reprezentovány ekvivalentními geometrickými imperfekcemi.

Tabulka C.2 uvádí hodnoty amplitudy podle typu dílce, které lze snadno odvodit. Tato kapitola však specifikuje, že může být nutné kombinovat různé typy geometrických imperfekcí. Kromě hlavní imperfekce by měly být jiné tvary imperfekcí reprezentovány (navíc) se 70 % jejich doporučené hodnoty amplitudy. SCIA Engineer umožňuje použít pouze jeden tvar vybočení jako imperfekci. V případě potřeby lze doprovodné geometrické imperfekce nahradit vhodnými fiktivními silami působícími na konstrukci.