Tweede-orde berekening

Een tweede-orde berekening houdt rekening met hoe een structuur zich vervormt terwijl er belastingen op worden uitgeoefend. Numeriek gezien  wordt de totale belasting verdeeld in kleinere delen en voor elk belastingsdeel verandert de stijfheid van de structuur.

Tweede-orde effecten worden ook P-Δ en p-δ effecten genoemd. In SCIA Engineer wordt voor deze effecten ook wel naar Geometrische niet-lineariteit verwezen.

Hieronder vind je enkele veelgestelde vragen van onze gebruikers over tweede-orde berekeningen. 

Wanneer moet ik een tweede-orde berekening uitvoeren?

Materiaalspecifieke Eurocode-delen (EC2, EC3, EC4, EC5,...) specificeren in hun hoofdstuk 5 (Constructie analyse) wanneer je een tweede orde-analyse moet uitvoeren. Voor staalconstructies wijzen lage waarden van de α_cr coëfficiënt op een hoge flexibiliteit (of slankheid) van de structuur. Hierdoor krijgen we een hoge gevoeligheid voor initiële imperfecties en laterale verplaatsingen.

Je bepaalt de α_cr coëfficiënt door de elastische kritische knikbelasting voor een globale instabiliteitsmodus (F_cr. ) te delen door de ontwerpbelasting op de constructie (F_Ed). Met andere woorden, we gebruiken de resultaten van de stabiliteitsanalyse om erachter te komen of we een tweede-orde berekening moeten uitvoeren of niet.

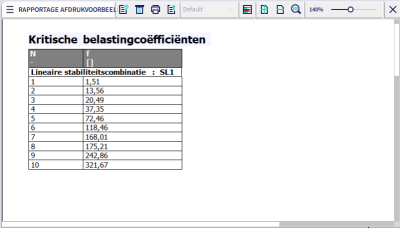
In SCIA Engineer creëren we stabiliteitscombinaties van de geselecteerde ontwerpcombinaties. Vervolgens verkrijgen we de kritische knikfactoren die overeenkomen met deze belastingscenario's. Deze factoren zijn eenvoudigweg multiplicatoren van de belasting die aanwezig is in de stabiliteitscombinatie. Omdat onze stabiliteitscombinaties de 'ontwerpbelasting' zijn, zijn deze factoren precies de α_cr coëfficiënten die we zoeken.

Het is ook belangrijk welke soort eindige-elementen analyse we uitvoeren om de interne krachten van het ontwerp te verkrijgen. Gaan we enkel een elastische analyse uitvoeren? Of maken we ook gebruik van plastische scharnieren om de momenten te herverdelen? Volgens EC3 moeten we de structuur ontwerpen met de resultaten van de tweede-orde berekening wanneer we een elastische analyse uitvoeren en als eender welke van onze α_cr lager zijn dan 10. In het geval van een plastische (bijv. scharnier) analyse, wijst elke α_cr die onder de 15 daalt op de noodzaak om naar de tweede-orde te overstappen. 

Hoe kan ik globale imperfecties invoegen volgens de code?

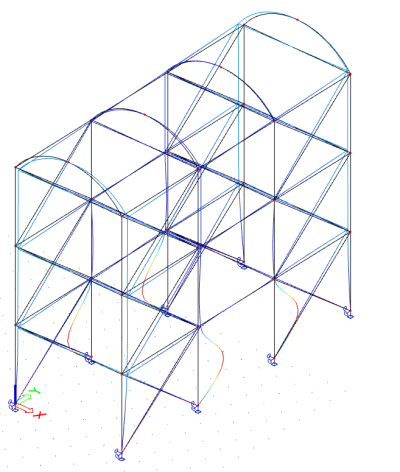
Geometrische imperfecties in een EE-model zorgen voor een correcte activering van de tweede orde-effecten tijdens een niet-lineaire analyse. Gebruikers die vertrouwd zijn met Hoofdstuk 5 van EC3 stellen vaak de vraag hoe ze rekening kunnen houden met de globale imperfecties of imperfecties van de structuur in SCIA Engineer.

Imperfecties zijn gedefinieerd bij de definitie van een niet-lineaire combinatie. Elke niet-lineaire combinatie kan een eigen imperfectie hebben. Dit is handig omdat verschillende belastingscenario's verschillende faalmodi veroorzaken. Deze faalmodi worden op hun beurt in een meer of mindere mate beïnvloed door een specifieke imperfectie-vorm.

 

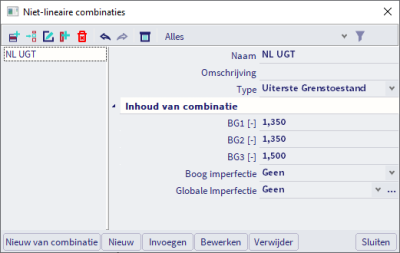
Globale imperfecties zijn gedefinieerd en opgeslagen in een specifieke bibliotheek die rechtstreeks kan worden benaderd vanuit het venster van de niet-lineaire combinaties of via Bibliotheken > Belastingsgevallen, combinaties > Globale Imperfecties.

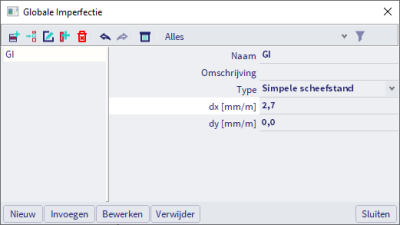
Om een globale imperfectie te definiëren als een uniforme zijwaartse scheefstand van de structuur, gebruik je het invoertype "Simpele scheefstand". Vervolgens definieer je dx en dy: de relatieve inclinatie volgens de globale X- en Y-assen. In EC3 is een formule beschikbaar in het Hoofdstuk 5.3.2, figuur 5.2 voor de hellingshoek, φ. Gebruik in de invoervelden in de niet-lineaire combinatiedialoog dx = 1000 * φx (of dx = 1000 * tan (φx), afhankelijk van hoe je de figuur interpreteert). De simpele scheefstand imperfectie is ideaal voor structuren die regelmatig in plattegrond en hoogte zijn. 

Zijn er verschillende invoermogelijkheden voor globale imperfecties?

Ja, hieronder vind je enkele mogelijkheden in SCIA Engineer:

• Scheefstandfuncties: als je de hellingswaarde wilt wijzigen en zelfs tekenen langs de hoogte (of lengte) van een structuur, kan je imperfectiefuncties gebruiken. Deze functies zijn handmatig gedefinieerde multilineaire krommen en je kan ze invoeren en opslaan via Bibliotheken > Structuur en analyse > Initiële vervormingen. 
  

   

• Imperfecties op basis van een belastingsgeval: SCIA Engineer berekent de vervorming van een structuur voor een belastinggeval dat je opgeeft. Daarnaast past onze software deze vervorming ook toe als een initiële imperfectie. Als je min of meer weet welke vorm van imperfectie je wilt verkrijgen, definieer je een belastingsgeval dat een dergelijke vervorming veroorzaakt. Je kan ook een belastingsgeval definiëren met een fractie van alle ontwerpbelastingen. Op deze manier ben je zeker dat alle mogelijke stabiliteitseffecten in de analyse worden weergegeven. 
  

• Een knikvorm uit de stabiliteitsberekening als imperfectie: je selecteert een stabiliteitscombinatie en één van de knikvormen om als imperfectie op de structuur aan te brengen. 

  

Hoe kan ik de lokale imperfectie invoegen volgens de norm?

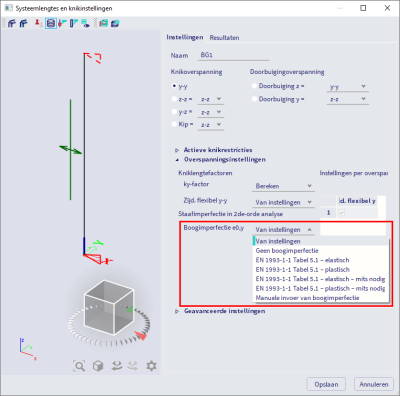
Zoals hierboven vermeld, worden imperfecties toegewezen per niet-lineaire combinatie. De meest praktische manier om de waarde van imperfecties toe te wijzen is om (via de instellingen van de combinatie) naar de knikinstellingen te verwijzen. Hiermee specifieer je via de kniksystemen welke elementen imperfecties moeten hebben. Het is vaak praktisch om enkel imperfecties toe te wijzen aan specifieke elementen die je nader wilt onderzoeken en niet aan alle elementen in de structuur. 

Zijn er verschillende invoermogelijkheden voor lokale imperfecties?

Ja, in plaats van te verwijzen naar knikgegevens, definieer je met SCIA Engineer lokale imperfecties rechtstreeks via de eigenschappen van de niet-lineaire combinatie. Houd er rekening mee dat de opgegeven kromming wordt toegepast op alle elementen in de structuur. 

 

Wat betekent de functionaliteit 'Geometische niet-lineariteit'?

Geometrische niet-lineariteit verwijst naar een tweede-orde berekening. Wanneer je een berekening uitvoert met deze instelling aangevinkt, zal de constructie vervormen wanneer de belasting wordt opgelegd en de belastingsstappen en numerieke methode voor de niet-lineaire berekening worden meegenomen zoals gedefinieerd in de instellingen voor de solver. Daarom zullen de resultaten verschillend zijn van deze voor een lineaire berekening, ongeacht of een initiële imperfectie is toegepast of niet. Het is echter raadzaam om imperfecties toe te passen om belangrijke niet-lineaire effecten goed in rekening te nemen.

Opmerking: Geometrische niet-lineairiteit is in rekening gebracht in de niet-lineaire berekening, die wordt uitgevoerd voor niet-lineaire combinaties. Tweede-orde effecten zijn niet aanwezig in de lineaire berekening: lineair opgeloste belastingsgevallen worden via superpositie samengenomen om tot resultaten voor lineaire combinaties te komen. In de niet-lineaire context geldt dit principe van superpositie niet, omdat de effecten van belastingen invloed hebben op de effecten van andere belastingen.

Hoe dien ik de amplitude voor de imperfectie te berekenen wanneer de knikvorm als imperfectie wordt gebruikt?

Raamwerken

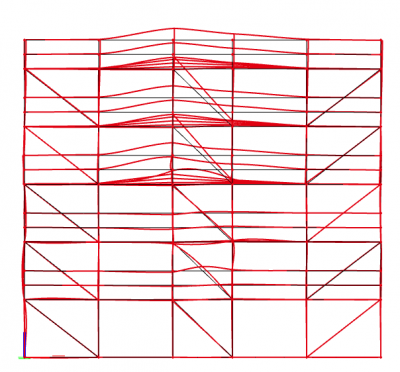
EN 1993-1-1 geeft richtlijnen in §5.3.2 (11) voor het berekenen van de amplitude van een unieke imperfectievorm die rechtstreeks is afgeleid van een stabiliteitsberekening (η_init). Deze methode is geldig voor raamwerken en vereist dat je de amplitude manueel afleidt en ingeeft in SCIA Engineer. De keuze van een knikvorm is ook aan jou.

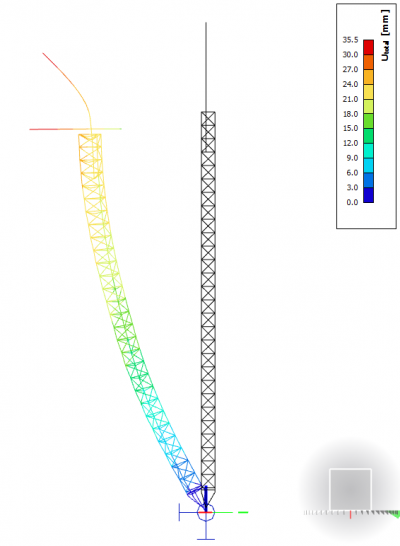
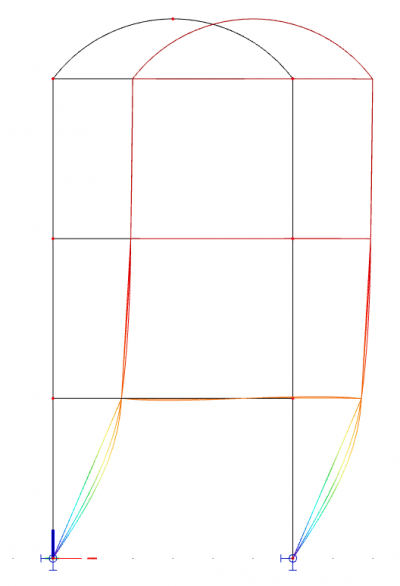
Deze methode om imperfecties te beheersen vereist dat je een belastingscombinatie definieert voor de stabiliteitsberekening zelf en dat je de bekomen instabiliteitsmodes visueel nakijkt. Je dient de laagste kritieke knikvorm te kiezen die de globale vervorming van de constructie geeft in de richting van het niet-lineaire belastingsscenario dat je onderzoekt. De instabiliteitsvorm en zijn amplitude worden ingegeven per niet-lineaire combinatie.
Voor de afleiding van de amplitude van de imperfectie, zal je wat inputs uit het EE model moeten verkrijgen, van resultaten van de lineaire en stabiliteitsberekening, evenals van de staalcontrole.

De imperfectie wordt als volgt afgeleid:

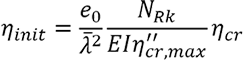
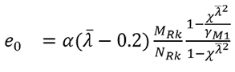
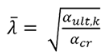
Met:

• η_cr: de vorm van de kritische elastische knikmode, vandaar dat de term ervoor de waarde van de amplitude is
• λ: de relatieve slankheid van de volledige constructie
• χ en α: reductie en imperfectiefactor, zoals afgeleid voor de kritische doorsnede; deze kunnen uit de staalcontrole worden verkregen
• α_ult,k: een factor die, indien toegepast op de belastingen in een lineair scenario, ervoor zou zorgen dat het meest gedrukte element zijn karakteristieke doorsnedeweerstand N_Rk bereikt
• α_cr: de kritische elastische knikfactor voor de stabiliteitscombinatie en geselecteerde knikvorm. Omwille van consistentie moet de stabiliteitscombinatie dezelfde belastingen bevatten als geanalyseerd in de niet-lineaire combinatie
• M_Rk: de karakteristieke momentweerstand van de kritische doorsnede, berekend voor de relevante doorsnedeklasse
• N_Rk: de karakteristieke normaalkrachtweerstand voor de kritische doorsnede
• EIη"_cr,max: (volledige term) is het buigmoment als gevolg van η_cr op de kritische doorsnede

Wanneer we bovenstaande interpreteren, zien we wat we moeten bepalen:

• de kritische doorsnede in de constructie (waar de belastingseffecten leiden tot een maximale utilisatieverhouding in lineaire context)
• het meest gedrukte element in de constructie

α_ult,k, M_Rk, N_Rk, χ en α kunnen worden verkregen via de staalcontrole. α_cr en (EIη"_cr,max) kunnen worden verkregen van de resultaten van de stabiliteitsberekening.

Platen

 

Voor constructies gemodelleerd met 2D-(plaat)elementen geldt een gelijkaardige procedure, maar de amplitude van de imperfecties moet worden bepaald volgens §C5 van EN 1993-1-5. Opnieuw dien je een niet-lineaire berekening met tweede-orde effecten en initiële imperfecties uit te voeren, om correct alle mogelijke knikfaalmodes te beschouwen.

Vanwege de veelzijdigheid van modellen met plaatelementen, kunnen in theorie alle faalmodes worden vastgelegd met passende:

• meshing;
• element formulering voor buiging en dwarskracht;
• en het opnemen van imperfecties.

Dit is anders dan voor raamwerken, waar bijkomende controles nodig zijn voor kip en torsieknik.

§C5 van EN 1993-1-5 geeft in essentie twee mogelijkheden voor de definitie van imperfecties:

• a. Een expliciete modellering van zowel geometrische als structurele imperfecties:
  • geometrische imperfecties kunnen worden benaderd als knikvormen, met amplitudes genomen als 80 % van de fabricagetoleranties;
  • structurele imperfecties (bV. residuele spanningen) kunnen worden weergegeven door een spanningspatroon dat wordt verwacht van het fabricageproces met amplitudes gelijk aan de verwachte (gemiddelde) waarden.
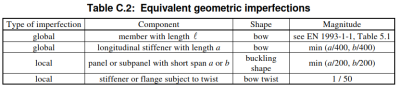
• b. Modellering van de imperfectievorm en amplitude volgens een vereenvoudigde benadering gegeven in tabel C.2. In dit geval worden zowel geometrische als structurele imperfecties weergegeven door equivalente geometrische imperfecties.
  Table C.2 geeft amplitudewaarden per type component die eenvoudig af te leiden zijn. Het hoofdstuk specifieert echter dat het kan dat verschillende types geometrische imperfecties gecombineerd dienen te worden: naast de hoofdimperfectie moeten andere imperfectievormen worden weergegeven (in addition) met 70 % van hun aanbevolen amplitudewaarde. SCIA Engineer laat enkel toe een enkele knikvorm te gebruiken als imperfectie: indien nodig kunnen begeleidende geometrische imperfecties worden vervangen door geschikte fictieve krachten die op de constructie werken.